FIND ALL ASYMPTOTES OF A  RATIONAL FUNCTION

The rational function will have three types of asymptotes.

i) Horizontal asymptote

ii) Vertical asymptote

iii) Slant asymptote.

i)  Horizontal asymptote :

Horizontal asymptotes are horizontal lines that the graph of the function approaches as x tends to +∞ or −∞.

A horizontal asymptote is a special case of a slant asymptote.

Let

deg N(x) = the degree of a numerator

and

deg D(x) = the degree of a denominator

Case 1 :

Degree of numerator = degree of denominator

y = leading coefficient of N(x)/leading coefficient of D(x).

Case 2 :

Degree of numerator < degree of denominator

y = 0, which is the x – axis.

Case 3 :

degree of numerator > degree of denominator

There is no horizontal asymptote.

ii)  Vertical Asymptotes :

The Vertical Asymptotes of a rational function are found using the zeros of the denominator.

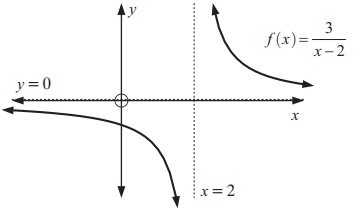
iii)  Oblique or slant asymptote :

A slant (oblique) asymptote occurs when the polynomial in the numerator is a higher degree than the polynomial in the denominator.

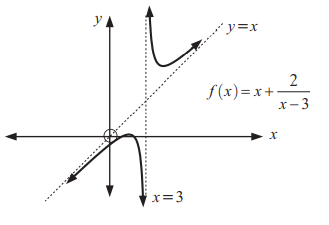
Find all asymptotes of the following function. (Don't have to graph it).

Problem 1 :

Solution :

i) Horizontal asymptote :

Highest exponent of numerator = Highest exponent of the denominator

So, the horizontal asymptote is at  y = 1

ii) Vertical asymptote :

x + 5 = 0

Vertical asymptote is at x = -5

Note :

Since we have horizontal asymptote, we don't have oblique asymptote.

Problem 2 :

Solution :

i) Horizontal asymptote :

Highest exponent of numerator < Highest exponent of the denominator

So, the horizontal asymptote is x-axis or y = 0.

ii) Vertical asymptote :

x² - 2 = 0

x² = 2

x = ±√2

Vertical asymptotes are at x = √2 and x = -√2.

Problem 3 :

Solution :

i) Horizontal asymptote :

Highest exponent of numerator > Highest exponent of the denominator

So, no horizontal asymptote, will have slant or oblique asymptote.

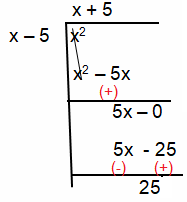
y = (x + 5) + [ 25/(x - 5) ]

So, the slant asymptote is y = x + 5

ii) Vertical asymptote :

x - 5 = 0

x = 5

Vertical asymptote is at x = 5.

Problem 4 :

Solution :

i) Slant asymptote :

Highest exponent of numerator > Highest exponent of the denominator

So, no horizontal asymptote, will have slant or oblique asymptote.

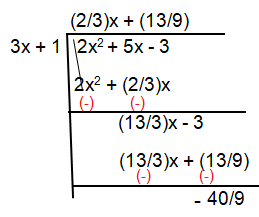
Slant asymptote is at y = (2/3)x + (13/9)

ii) Vertical asymptote :

x - 1 = 0

x = 1

Vertical asymptote is at x = 1

Problem 5 :

Solution :

i) Horizontal asymptote :

Highest exponent of numerator = Highest exponent of the denominator

y = 7/2

So, the horizontal asymptote is at y = 7/2.

ii) Vertical asymptote :

2x² - 18 = 0

2x² = 18

x² = 9

x = ±3

Vertical asymptotes are at x = 3 and x = -3

Problem 6 :

Solution :

i) Slant asymptote :

Highest exponent of numerator > Highest exponent of the denominator

So, no horizontal asymptote, will have slant or oblique asymptote.

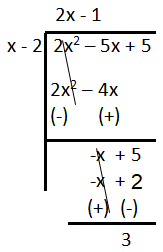
y = (2x-1) + [3/(x-2)]

So, the slant asymptote is at y = 2x - 1.

ii) Vertical asymptote :

x - 2 = 0

x = 2

Vertical asymptote is at x = 2.

Problem 7 :

Solution :

i) Horizontal asymptote :

Highest exponent of numerator < Highest exponent of the denominator

So, the horizontal asymptote is x-axis or y = 0.

ii) Vertical asymptote :

x - 3 = 0

x = 3

Vertical asymptote is at x = 3.

Problem 8 :

Solution :

i) Horizontal asymptote :

Highest exponent of numerator < Highest exponent of the denominator

So, the horizontal asymptote is x-axis or y = 0.

ii) Vertical asymptote :

x⁴ - 81 = 0

x⁴ = 81

x⁴ = 3⁴

x = -3 and x = 3

Vertical asymptotes are at x = -3 and x = 3.

Problem 9:

Solution :

i) Slant asymptote :

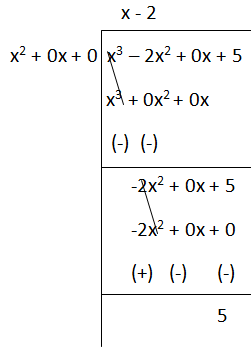
y = (x - 2) + (5/x²)

So, the slant asymptote is at y = x - 2.

ii) Vertical asymptote :

x² = 0

x = 0

Vertical asymptote is at x = 0