FIND ABSOLUTE VALUE OPPOSITE AND RECIPROCALS

Evaluate the value of each expression :

Problem 1 :

f(x) = -4|x - 2| + 5 at x = -3/2 find f(-3/2)

Solution :

Given that, f(x) = -4|x - 2| + 5 at x = -3/2

Applying the value of x, we get 

f(-3/2) = -4|(-3/2) - 2| + 5

= -4|(-3 - 4)/2| + 5

= -4|-7/2| + 5

= -4(7/2) + 5

= -2(7) + 5

= -14 + 5

= -9

Problem 2 :

f(x) = 5|x + 1| + 2 at x = 2 find f(2)

Solution :

Given that, f(x) = 5|x + 1| + 2, x = 2

f(2) = 5|2 + 1| + 2

= 5|3| + 2

= 5(3) + 2

= 15 + 2

= 17

Problem 3 :

Copy and complete the statement using <, >, or =.

a)  ∣ −2 ∣   ____  −1

b)  −7  _____ ∣ 6 ∣

c)  ∣ 10 ∣ ____  11

d) 9 ___  ∣ −9 ∣

Solution :

a)  ∣ −2 ∣   ____  −1

|-2| = 2

Comapring 2 and -1, 2 is greater. Then ∣ −2 ∣  > −1

b)  −7  _____ ∣ 6 ∣

|6| = 6

Comparing -7 and 6, 6 is greater.

-7 < |6|

c)  ∣ 10 ∣ ____  11

Comparing 10 and 11, 11 is greater.

|10| < 11

d) 9 ___  ∣ −9 ∣

|-9| = 9

Here 9 and |9| are equal. Then 9 = |-9|

Problem 4 :

The freezing point is the temperature at which a liquid becomes a solid.

a. Which substance in the table has the lowest freezing point?

b. Is the freezing point of mercury or butter closer to the freezing point of water, 0°C?

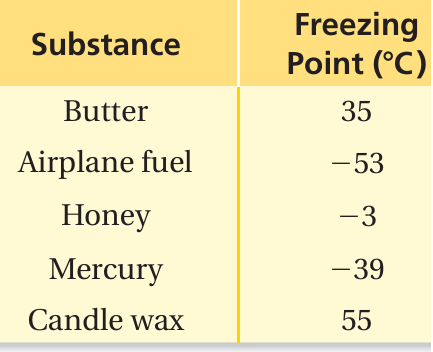
Solution :

a. Graph each freezing point.

Airplane fuel has the lowest freezing point, −53°C.

b. The freezing point of water is 0°C, so you can use absolute values.

Mercury: ∣ −39 ∣= 39 Butter: ∣ 35 ∣= 35

Because 35 is less than 39, the freezing point of butter is closer to the freezing point of water

Problem 5 :

Which expression does not belong with the other three? Explain your reasoning.

∣ 6 ∣      6      −6      ∣ −6 ∣

Solution :

∣ 6 ∣ = 6

6 = 6

−6 = -6

∣ −6 ∣ = 6

So, -6 does not belongs to the other three.

Problem 6 :

Copy and complete the statement using <, >, or =.

a) 2 ____ ∣−5∣

b) ∣−4∣  ___  7

c)  −5 ____ ∣−9∣

d) ∣−4∣  ____ −6

e) ∣−1∣  ___  ∣−8∣

f)  ⏐5⏐ ___  ∣−5∣

Solution :

a) 2 ____ ∣−5∣

|-5| = 5

Comparing 2 and 5, 5 is greater.

2 < ∣−5∣

b) ∣−4∣  ___  7

|-4| = 4

Comparing 4 and 7, 7 is greater.

∣−4∣  <  7

c)  −5 ____ ∣−9∣

|-9| = 9

Comparing -5 and 9, 9 is greater.

−5 < ∣−9∣

d) ∣−4∣  ____ −6

|-4| = 4

Comparing 4 and -6, 4 is greater.

∣−4∣ > −6

e) ∣−1∣  ___  ∣−8∣

|-1| = 1

|-8| = 8

Comparing 1 and 8, 8 is greater.

∣−1∣ < ∣−8∣

f)  ⏐5⏐ ___  ∣−5∣

|-5| = 5

Both are equal.

⏐5⏐ = ∣−5∣

Problem 7 :

Order the values from least to greatest.

a) 8, ∣ 3 ∣ , −5, ∣ −2 ∣ , −2

b) ∣ −6 ∣ , −7, 8, ∣ 5 ∣ , −6

c) −12, ∣ −26 ∣ , −15, ∣ −12 ∣ , ∣ 10 ∣

d) ∣ −34 ∣ , 21, −17, ∣ 20 ∣ , ∣ −11 ∣

Solution :

a)

8, ∣ 3 ∣ , −5, ∣ −2 ∣ , −2

|3| = 3

|-2| = 2

8, 3, -5, 2, -2

Comparing the numbers and arranging from least to greatest, we get

-5, -2, 2, 3, 8

b)

∣ −6 ∣ , −7, 8, ∣ 5 ∣ , −6

|-6| = 6

|5| = 5

6, -7, 8, 5, -6

Comparing the numbers and arranging from least to greatest, we get

-7, -6, 5, 6, 8

c) 

−12, ∣−26∣ , −15, ∣−12∣ , ∣10∣

|-26| = 26

|-12| = 12

|10| = 10

-12, 26, -15, 12, 10

Comparing the numbers and arranging from least to greatest, we get

-15, -12, 10, 12, 26

d)

∣−34∣ , 21, −17, ∣20∣ , ∣−11∣

|-34| = 34

|20| = 20

|-11| = 11

34, 21, -17, 20, 11

Comparing the numbers and arranging from least to greatest, we get

-17, 11, 20, 21, 34