FIND ABSOLUTE MAXIMUM AND MINIMUM VALUE OF A FUNCTION`

Problem 1 :

The function g is given by

g(x) = 4x³ + 3x² - 6x + 1

what is the absolute minimum value of g on the closed interval [-2, 1] ?

A)  -7        B)  -3/4       C)  0        D)  2       E)  6

Solution :

g(x) = 4x³ + 3x² - 6x + 1

g'(x) = 4(3x²) + 3(2x) - 6(1) + 0

g'(x) = 12x² + 6x - 6

g'(x) = 0

12x² + 6x - 6 = 0

6(2x² + x - 1) = 0

(x + 1)(2x - 1) = 0

x = -1 and x = 1/2

Critical numbers are -1 and 1/2.

Applying x = -2

g(x) = 4x³ + 3x² - 6x + 1

g(-2) = 4(-2)³ + 3(-2)² - 6(-2) + 1

= -32 + 12 + 12 + 1

= -7

Applying x = -1

g(-1) = 4(-1)³ + 3(-1)² - 6(-1) + 1

= -4 + 3 + 6 + 1

= 6

Applying x = 1/2

g(1/2) = 4(1/2)³ + 3(1/2)² - 6(1/2) + 1

= 1/2 + 3/4 - 3 + 1

= 1/2 + 3/4 - 2

= (2+3-8)/4

= -3/4

Applying x = 1

g(1) = 4(1)³ + 3(1)² - 6(1) + 1

= 4 + 3 - 6 + 1

= 8 - 6

= 2

Minimum value is at (-2, -7). So, option A is correct.

Problem 2 :

Find the absolute maximum and absolute minimum of the function under the given interval.

f(x) = 4x³ − 108x ; [0,5]

Solution :

f(x) = 4x³ − 108x

f'(x) = 4(3x²) - 108(1)

f'(x) = 12x² - 108

f'(x) = 0

12(x² - 9) = 0

x² - 9 = 0

(x + 3)(x - 3) = 0

x = -3 and x = 3

-3 is not in the interval.

f(0) = 4(0)³ − 108(0) ==> 0

f(3) = 4(3)³ − 108(3) ==> -216

f(5) = 4(5)³ − 108(5) ==> -40

Absolute maximum is at (0, 0) and absolute minimum is at (3, -216).

Problem 3 :

Find the absolute maximum and absolute minimum

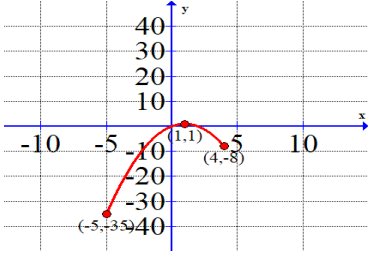
Solution :

Minimum are at (-5, -35) and (4, -8)

Maximum is at (1, 1).

Absolute minimum is at (-5, -35) and absolute maximum is at (1 ,1).

Problem 4 :

Find the absolute maximum and absolute minimum

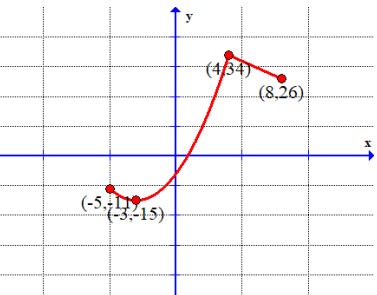
Solution :

Absolute minimum is at (-3, -15)

Absolute maximum is at (4, 34).

Problem 5 :

Let f be the function given by f(x) = x - 2 sin x for 0 ≤ x ≤ 2π

a) Find the intervals on which f is increasing and decreasing.

b) Find the absolute minimum and maximum value on the given interval.

Solution :

f(x) = x - 2 sin x

f'(x) = 1 - 2 cos x

f'(x) = 0

1 - 2 cos x = 0

2 cos x = 1

cos x = 1/2

x = cos^-1 (1/2)

x = π/3 and 5π/3

Dividing into intervals :

(0, π/3) (π/3, 5π/3) and (5π/3, 2π)

Finding increasing and decreasing interval :

(0, π/3)

x = π/4

f'(π/4) = 1 - 2 cos (π/4)

= 1 - 2 (√2/2)

= 1 - √2 < 0 (decreasing)

(π/3, 5π/3)

x = π/2

f'(π/2) = 1 - 2 cos (π/2)

= 1 - 0

= 1 > 0 (increasing)

(5π/3, 2π)

x = 330 degree

f'(π/2) = 1 - 2 cos (330)

= 1 - 2sin 60

= 1 - 2(√3/2)

= 1 - √3 (decreasing)

Decreasing on (0, π/3) U(5π/3, 2π) and increasing on (π/3, 5π/3).

Critical numbers are x = π/3 and 5π/3.

f(x) = x - 2 sin x

f(0) = 0 - 2 sin 0 ==> 0

f(π/3) = π/3 - 2 sin (π/3) ==> π/3 - √3

f(5π/3) = 5π/3 - 2 sin (5π/3) ==> 5π/3 + √3

So, absolute maximum is 5π/3 + √3 and absolute minimum is π/3 - √3.