FACTORING TRINOMIALS WHEN A IS 1

Write each trinomial in factored form (as the product of two binomials).

Problem 1 :

p² + 14p + 48

Solution :

= (p + 6) (p + 8)

Problem 2 :

n² + 10n + 16

Solution :

= (n + 2) (n + 8)

Problem 3 :

p² + 14p + 40

Solution :

= (p + 4) (p + 10)

Problem 4 :

r² + 9r + 18

Solution :

= (r + 3) (r + 6)

Problem 5 :

p² - 8p + 7

Solution :

= (p - 1) (p - 7)

Problem 6 :

b² - 9b + 14

Solution :

= (b - 2) (b - 7)

Problem 7 :

b² - 8b + 15

Solution :

= (b - 3) (b - 5)

Problem 8 :

m² - 16m + 63

Solution :

= (m - 7) (m - 9)

Problem 9 :

k² - 4k – 60

Solution :

= (k + 6) (k - 10)

Problem 10 :

m² + m – 6

Solution :

= (m - 2) (m + 3)

Problem 11 :

p² - 2p – 15

Solution :

= (p + 3) (p - 5)

Problem 12 :

r² + r – 20

Solution :

= (r - 4) (r + 5)

Problem 13 :

The area (in square centimeters) of a square coaster can be represented by

d² + 8d + 16

a. Write an expression that represents the side length of the coaster.

b. Write an expression for the perimeter of the coaster.

Solution :

a) 

Area = d² + 8d + 16

= d² + 4d + 4d + 16

Factoring d from first two terms and factoring 4 from the next two terms, we get

= d(d + 4) + 4(d + 4)

= (d + 4)(d + 4)

So, side length of square is (d + 4) cm

b)  Perimeter of coaster = 4(side length)

= 4(d + 4)

= (4d + 16) cm

Problem 14 :

The polynomial represents the area (in square feet) of the square playground.

a. Write a polynomial that represents the side length of the playground.

b. Write an expression for the perimeter of the playground.

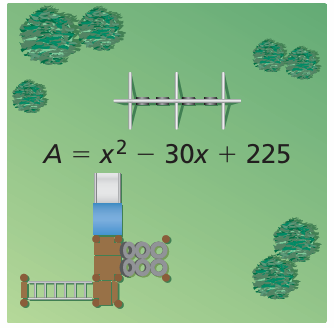
Solution :

a)

Area = x² - 30x + 225

= x² - 15x - 15x + 225

= x(x - 15) - 15(x - 15)

= (x - 15)(x - 15)

So, side length of the square is (x - 15) cm.

b) 

Perimeter of square = 4(side length)

= 4(x - 15)

= (4x - 60) cm

Problem 15 :

Tell whether the polynomial can be factored. If not, change the constant term so that the polynomial is a perfect square trinomial.

a. w² + 18w + 84

b. y² − 10y + 23

Solution :

a.

= w² + 18w + 84

84 = 7 x 12 (won't work)

84 = 4 x 21 (won't work)

To make the given quadratic as perfect square, we need to have 81 as constant since we have 18 as a middle term.

= w² + 9w + 9w + 81

= w (w + 9) + 9(w + 9)

= (w + 9)(w + 9)

= (w + 9)²

b.

y² − 10y + 23

23 = 1 x 23 (won't work)

To make the given quadratic as perfect square, we need to have 25 as constant since we have -10 as a middle term.

= y² − 5y - 5y + 25

= y(y - 5) - 5(y - 5)

= (y - 5)(y - 5)

= (y - 5)²

Problem 16 :

The width of a calculator can be represented by (3x + 1) inches. The length of the calculator is twice the width. Write a polynomial that represents the area of the calculator.

Solution :

Width of the calculator = 3x + 1

length = 2(3x + 1)

Area of calculator = (3x + 1) 2(3x + 1)

= 2(3x + 1)²

= 2[(3x)² + 2(3x)(1) + 1²]

= 2 (9x² + 6x + 1)

So, the required area of the calculator is 2 (9x² + 6x + 1).