FACTOR THE POLYNOMIAL INTO LINEAR FACTORS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Problem 1 :
a³ + 3a² - a – 3
Solution :
= a³ + 3a² - a – 3
Grouping the first two terms and last two terms.
= (a³ + 3a²) + (- a – 3)
= a² (a + 3) – 1(a + 3)
= (a² - 1) (a + 3)
= (a2 - 12) (a + 3)
Using the algebraic identity, we get
= (a + 1) (a - 1) (a + 3)
Problem 2 :
5x² - 15x + 10
Solution :
= 5x² - 15x + 10
= 5x² - 10x – 5x + 10
= 5x(x - 2) – 5(x - 2)
= (5x - 5) (x - 2)
Factoring 5, we get
= 5(x - 1) (x - 2)
Problem 3 :
b³ - 4b
Solution :
= b³ - 4b
= b (b² - 4)
(a² - b²) = (a + b) (a - b)
= b(b + 2) (b - 2)
Problem 4 :
4ax² + 4ax – 24a
Solution :
= 4ax² + 4ax – 24a
= 4a(x² + x - 6)
= 4a(x² - 2x + 3x - 6)
= 4a [x(x - 2) + 3(x - 2)]
= 4a (x - 2) (x + 3)
Problem 5 :
12c² - 3
Solution :
= 12c² - 3
= 3(4c² - 1)
(a² - b²) = (a + b) (a - b)
= 3(2c + 1) (2c - 1)
Problem 6 :
x4 – 81
Solution :
= x4 – 81
(a² - b²) = (a + b) (a - b)
= (x² + 9) (x² - 9)
= (x² + 9) (x + 3) (x - 3)
Problem 7 :
x4 – 16
Solution :
= x4 – 16
(a² - b²) = (a + b) (a - b)
= (x² + 4) (x² - 4)
= (x² + 4) (x + 2) (x - 2)
Problem 8 :
2x³ + 13x² + 15x
Solution :
= 2x³ + 13x² + 15x
= 2x³ + 10x² + 3x² + 15x
= 2x²(x + 5) + 3x(x + 5)
= (2x² + 3x) (x + 5)
= x(2x + 3) (x + 5)
Problem 9 :
4x³ - 10x² + 6x
Solution :
= 4x³ - 10x² + 6x
= 4x³ - 4x² - 6x² + 6x
= 4x²(x - 1) – 6x(x - 1)
= (4x² - 6x) (x - 1)
= 2x(2x – 3) (x - 1)
Problem 10 :
z4 – 12z² + 27
Solution :
= z4 – 12z² + 27
= z4 – 3z² - 9z² + 27
= z²(z² - 3) - 9(z² - 3)
= (z² - 9) (z² - 3)
= (z + 3) (z - 3) (z² - 3)
Problem 11 :
(c + 2)² - 1
Solution :
= (c + 2)² - 1
= c² + 4c + 4 – 1
= c² + 4c + 3
= c² + c + 3c + 3
= c(c + 1) + 3(c + 1)
= (c + 3) (c + 1)
Problem 12 :
4 – (y - 1)²
Solution :
= 4 – (y - 1)²
= 22 - (y - 1)²
Using the algebraic identity, we get
= (2 + (y - 1))(2 - (y - 1))
= (2 + y - 1) (2 - y + 1)
= (y + 1) (3 - y)
Problem 13 :
x²y – 16y
Solution :
= x²y – 16y
= y(x² - 16)
(a² - b²) = (a + b) (a - b)
= y(x + 4) (x - 4)
Problem 14 :
3(x - 1)² - 12
Solution:
= 3(x - 1)² - 12
= 3(x² + 1 – 2x) – 12
= 3x² + 3 – 6x – 12
= 3x² - 6x – 9
= 3x² + 3x – 9x – 9
= 3x(x + 1) – 9(x + 1)
= (3x - 9) (x + 1)
= 3(x - 3) (x + 1)
Problem 15 :
9 – 9(x + 2)²
Solution :
= 9 – 9(x + 2)²
Factoring 9, we get
= 9[1 – (x + 2)²]
= 9 [12 – (x + 2)2]
= 9 [(1+ x + 2) (1 - x - 2)]
= -9 [(x + 3) (x + 1)]
= -9 (x + 3) (x + 1)
Problem 16 :
The area (in square feet) of a rectangular lighted dance floor can be represented by 8x2 + 22x + 5. Write the expressions that represent the dimensions of the dance floor.

Solution :
Area of the rectangular floor = 8x2 + 22x + 5
= 8x2 + 20x + 2x + 5
= 4x(2x + 5) + 1(2x + 5)
= (4x + 1)(2x + 5)
So, the dimensions of the floor are 4x + 1 and 2x + 5.
Problem 17 :
Describe and correct the error in factoring the polynomial.
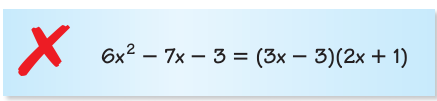
Solution :
= 6x2 - 7x - 3
= 6x2 - 9x + 2x - 3
= 3x(2x - 3) + 1(2x - 3)
= (3x + 1)(2x - 3)
The factors are incorrect.
Problem 18 :
Factor the polynomial.
a) 40k3 + 6k2 − 4k
b) 6x2 + 5xy − 4y2
c) 18m3 + 39m2n − 15mn
Solution :
a) 40k3 + 6k2 − 4k
= 2k2 (20k2 + 3k - 2)
= 2k2 (20k2 + 8k - 5k - 2)
= 2k2 [4k(5k + 2) - 1(5k + 2)]
= 2k2 (4k - 1) (5k + 2)
b) 6x2 + 5xy − 4y2
= 6x2 + 8xy - 3xy − 4y2
= 2x(3x + 4y) - y(3x + 4y)
= (2x - y)(3x + 4y)
c) 18m3 + 39m2n − 15mn2
= 3m(6m2 + 13mn − 5n2)
= 3m(6m2 - 2mn + 15mn − 5n2)
= 3m[2m(3m - n) + 5n(3m - n)]
= 3m[ (2m + 5n)(3m - n) ]
= 3m (2m + 5n)(3m - n)
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling