FACES EDGES VERTICES

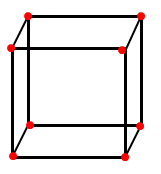
What are Vertices ?

• A point where two or more line segments meet is known as a vertex.
• The plural of vertex is vertices.
• In simpler words, we can say that a vertex is a corner.

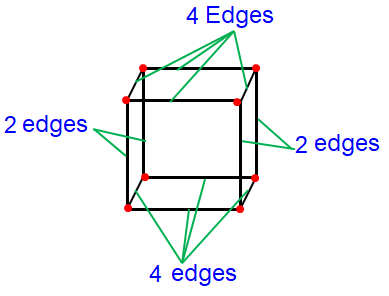
What are edges ?

An edge in a shape can be defined as a point where two faces meet.

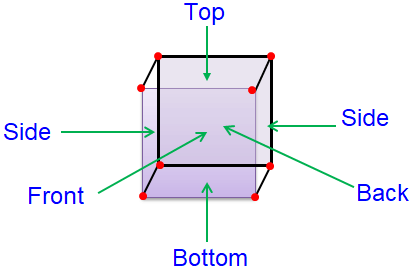
What are faces ?

Every individual flat surface of a solid is called its face. Solids have more than one face.

Write the number of faces, edges, and vertices, and identify each 3D shape.

Problem 1 :

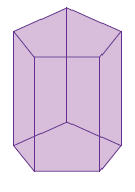
Solution :

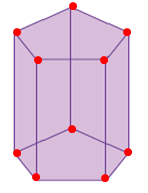
Number of vertices :

Marking vertices, number of vertices for a pentagonal prism is 10.

Number of faces :

Side = 5 faces

Top and bottom = 2 faces

Total faces = 7

Number of edges :

Edges = 15

Problem 2 :

Solution :

Number of vertices :

One vertex at the top.

Number of faces :

Curved face = 1

bottom face = 1

Total faces is 2.

Number of edges :

A cone has one flat surface and one curved surface. Number of edges of cone is 1.

Problem 3 :

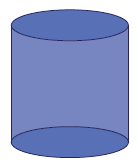
Solution :

Number of vertices :

There is no vertices.

Number of faces :

Curved face = 1

bottom face = 1

Top face = 1

Total faces is 3.

Number of edges :

Curved surface is connected with top face to the bottom face, so number of edges is 2.

Problem 4 :

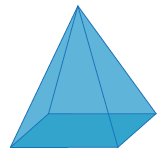
Solution :

Number of vertices :

Number of corners for rectangle = 4, at top we have 1

Total vertices = 4 + 1 => 5

Number of faces :

Curved face = 4

bottom face = 1

Total faces is 5.

Number of edges :

Number of edges = 8

Problem 5 :

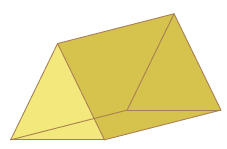
Solution :

Number of vertices :

Number of corners for rectangle = 4, at top = 2

Total vertices = 4 + 2 => 6

Number of faces :

Front face = 1

back face = 1

side face = 2

bottom face = 1

Total faces = 1 + 1 + 2 + 1 ==> 5

Total faces is 5.

Number of edges :

Number of edges = 9

Problem 6 :

Solution :

Number of vertices :

Number of vertices = 0

Number of faces :

There is curved surface. So, total faces = 1.

Number of edges :

Number of edges = 0

Problem 7 :

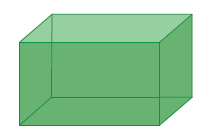
Solution :

Number of vertices :

Number of rectangle at the top = 4

Number of rectangle at bottom = 4

Number of vertices = 4 + 4 ==> 8

Number of faces :

Side faces = 2

Top and bottom = 2

Front and back = 2

Total faces = 2 + 2 + 2 ==> 6

Number of edges :

Number of edges = 12

Problem 8 :

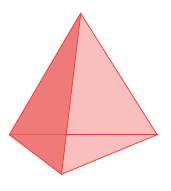
Solution :

Number of vertices :

Number of corners in triangle = 3

At top, we have 1

Total vertices = 3 + 1 ==> 4

Number of faces :

Side faces = 3

bottom = 1

Total faces = 3 + 1 ==> 4

Number of edges :

Number of edges = 6