EXTERIOR ANGLE THEOREM

An interior angle of a triangle is formed by two sides of the triangle. An exterior angle is formed by one side of the triangle and the extension of an adjacent side.

Each exterior angle has two remote interior angles. A remote interior angle is an interior angle that is not adjacent to the exterior angle.

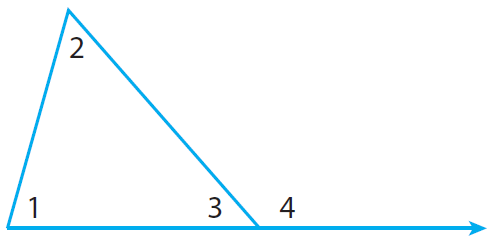
Extend the base of the triangle and label the exterior angle as ∠4.

The Triangle Sum Theorem states :

m∠1 + m∠2 + m∠3 = 180 -----(1)

So, m∠3 + m∠4 = 180 -----(2)

(2) = (1)

m∠1 + m∠2 + m∠3 = m∠3 + m∠4

m∠1 + m∠2 = m∠4

Problem 1 :

Find the value of x.

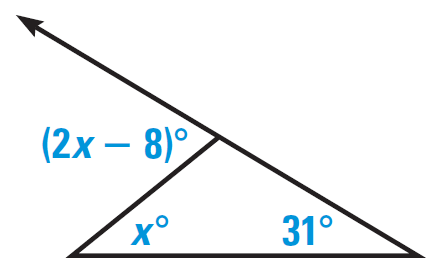
Solution :

Using exterior angle theorem :

2x - 8 = x + 31

Subtracting x on both sides.

2x - x - 8 = 31

Add 8 on both sides.

x = 31 + 8

x = 39

Problem 2 :

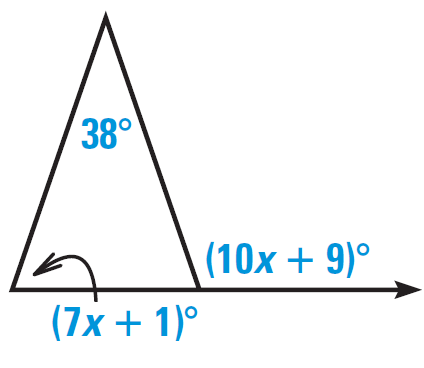
Solution :

Using exterior angle theorem :

7x + 1 + 38 = 10x + 9

7x + 39 = 10x + 9

Subtracting 39 on both sides.

7x - 10x + 39 = 9

Subtracting 39 on both sides.

-3x = 9 - 39

-3x = - 30

x = 10

Problem 3 :

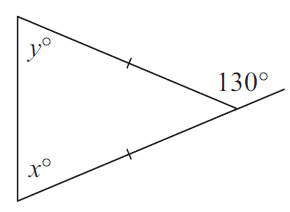
Solution :

Since the given triangle is isosceles triangle,

x = y

x + y = 130

x + x = 130

2x = 130

x = 130/2

x = 65

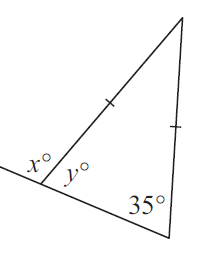
Problem 4 :

Solution :

Since the given triangle is isosceles triangle,

∠y = 35

x + y = 180

x + 35 = 180

x = 180 -35

x = 145

Problem 5 :

Find m∠ACB, m∠BCD and m∠DCE.

Solution :

In triangle ABC,

∠A + ∠B + ∠ACB = 180

78 + 58 + ∠ACB = 180

136 + ∠ACB = 180

∠ACB = 180 - 136

∠ACB = 44

In triangle DCE,

∠D + ∠E + ∠ECD = 180

60 + 85 + ∠ECD = 180

∠ECD = 180 - 145

∠ECD = 35

∠ACB + ∠BCD + ∠DCE = 180

44 + 35 + ∠BCD = 180

∠BCD = 180 - 79

∠BCD = 101

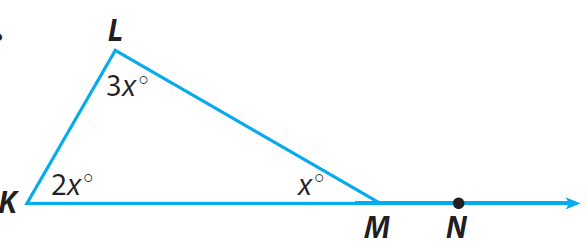
Problem 6 :

Find m∠K, m∠L, m∠KML, m∠LMN.

Solution :

In triangle LKM :

∠K + ∠L + ∠KML = 180

2x + 3x + x = 180

6x = 180

x = 180/6

x = 30

∠L = 3x ==> 3(30) ==> 90

∠K = 2x ==> 2(30) ==> 60

∠KML = x ==> 30

∠LMN = 180 - 30 ==> 150

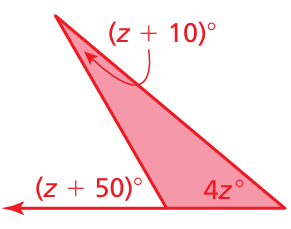
Problem 7 :

Find the measure of the exterior angle. Solve for z.

Solution :

Sum of remote interior angle = Exterior angle

z + 10 + 4z = z + 50

5z + 10 = z + 50

5z - z = 50 - 10

4z = 40

z = 40/4

z = 10

So, the value of z is 10.

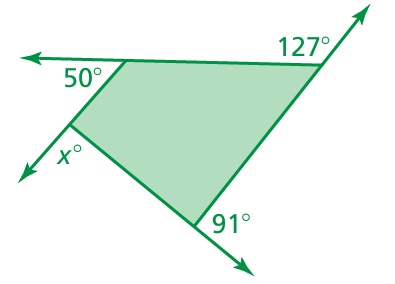
Problem 8 :

Find the measures of the exterior angles of each polygon. Solve for x.

Solution :

Sum of exterior angle of polygon = 360

x + 50 + 127 + 91 = 360

x + 268 = 360

x = 360 - 268

x = 92

So, the value of x is 92.

\Problem 9 :

Find the measures of the exterior angles of each polygon. Solve for z.

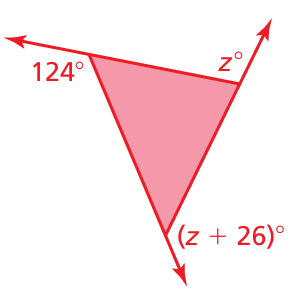
Solution :

Sum of exterior angle of polygon = 360

z + 124 + z + 26 = 360

2z + 150 = 360

2z = 360 - 150

2z = 110

z = 210/2

z = 105

So, the value of z is 105.

Problem 10 :

Find the measures of the exterior angles of the polygon.

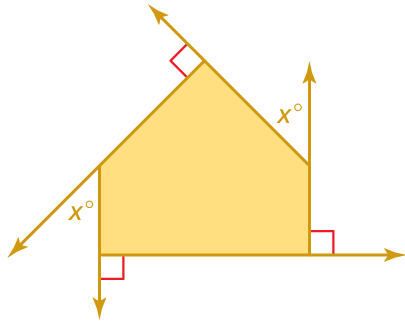
Solution :

Sum of exterior angle of polygon = 360

x + 90 + x + 90 + 90 = 360

2x + 270 = 360

2x = 360 - 270

2x = 90

x = 90/2

x = 45

So, the value of x is 45.

Problem 11 :

In FGH, m∠F = 42 and an exterior angle at vertex H has a measure of 104. What is m∠G?

a) 34      b) 62     c) 76     d) 146

Solution :

m∠H =  m∠F +  m∠G

104 = 42 +  m∠G

m∠G = 104 - 42

m∠G = 62

So, option b is correct.

Problem 12 :

In the diagram below of ABC, side BC is extended to point D, m∠A = x, m∠B = 2x + 15, and m∠ACD =5x + 5.

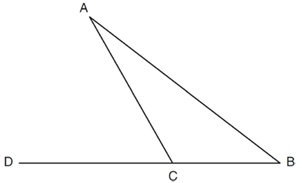
What is m∠B?

a) 5       b) 20     c) 25       d) 55

Solution :

m∠A = x, m∠B = 2x + 15 are interior angles.

m∠ACD = 5x + 5 is exterior angle.

m∠A + m∠B = m∠ACD

x + 2x + 15 = 5x + 5

3x + 15 = 5x + 5

3x - 5x = 5 - 15

-2x = -10

x = 10/2

x = 5

Applying the value of x in 2x + 15, we get

m∠B = 2(5) + 15

= 10 + 15

= 25

So,  m∠B is 25. Option c is correct.