EXPRESSING RELATIONS IN DIFFERENT FORMS

Express the following relations as

i)  a table

ii) a graph

iii)  a mapping

Then, state the domain and range of the relation. 

Problem 1 :

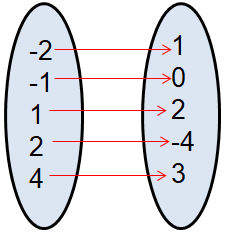
{(-2, 1), (-1, 0), (1, 2), (2, -4), (4, 3)}

Solution :

Given, {(-2, 1), (-1, 0), (1, 2), (2, -4), (4, 3)}

Table :

Graph :

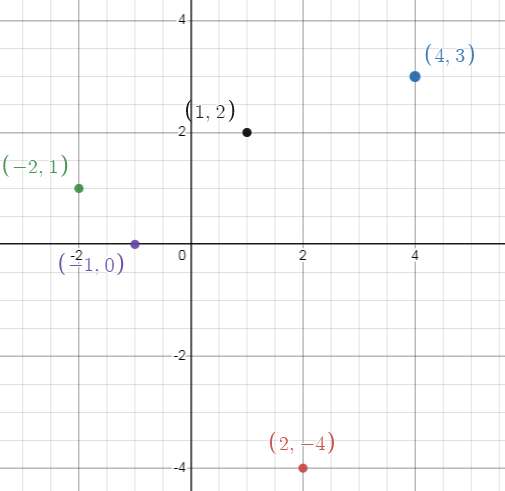
Mapping a diagram :

Domain :

{-2, -1, 1, 2, 4}

Range :

{1, 0, 2, -4, 3}

Problem 2 :

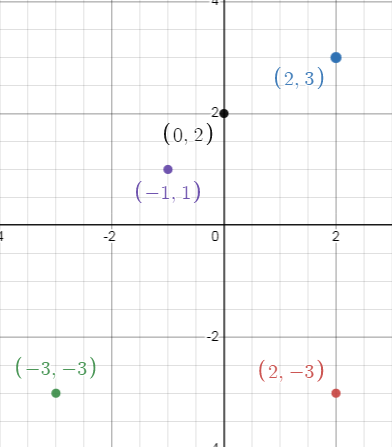
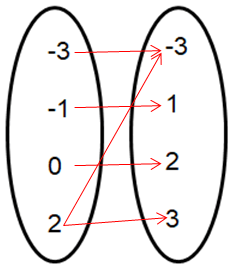
{(-3, -3), (-1, 1), (0, 2), (2, -3), (2, 3)}

Solution :

Given, {(-3, -3), (-1, 1), (0, 2), (2, -3), (2, 3)}    

Table :

If x = -3 and y = -3

x = -1 and y = 1

x = 0 and y = 2

x = 2 and y = -3

x = 2 and y = 3

Graph :

Mapping a diagram :

Domain :

{-3, -1, 0, 2}

Range :

{-3, 1, 2, 3}

This relation is not a function.

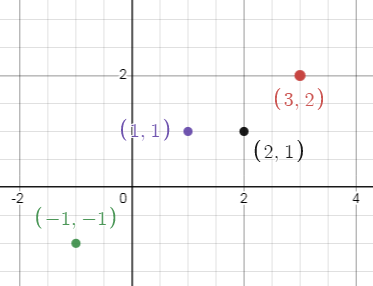
Problem 3 :

Express the relation

{(-1, -1), (1, 1), (2, 1), (3, 2)}

as

i)  a table

ii) a graph

iii)  a mapping

Then, state the domain and range of the relation. 

Solution :

Table :

If x = -1 and y = -1

x = 1 and y = 1

x = 2 and y = 1

x = 3 and y = 2

Graph :

Mapping a diagram :

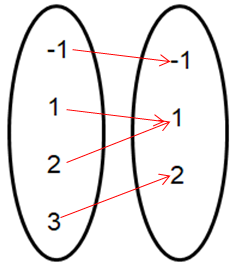
Domain :

(-1, 1, 2, 3)

Range :

(-1, 1, 2)

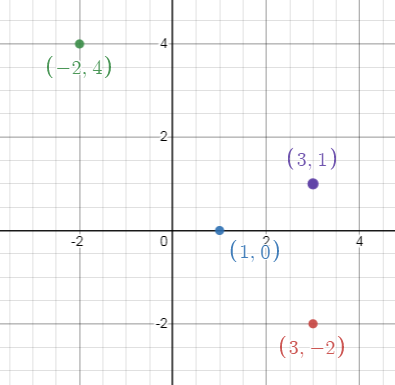
Problem 4 :

{(3, -2), (1, 0), (-2, 4), (3, 1)}

Solution :

Table :

If x = 3 and y = -2

x = 1 and y = 0

x = -2 and y = 4

x = 3 and y = 1

Graph :

Mapping a diagram :

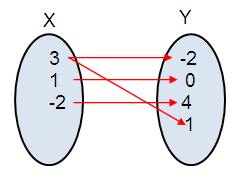
Domain :

{3, 1, -2}

Range :

{-2, 0, 4, 1}

Problem 5 :

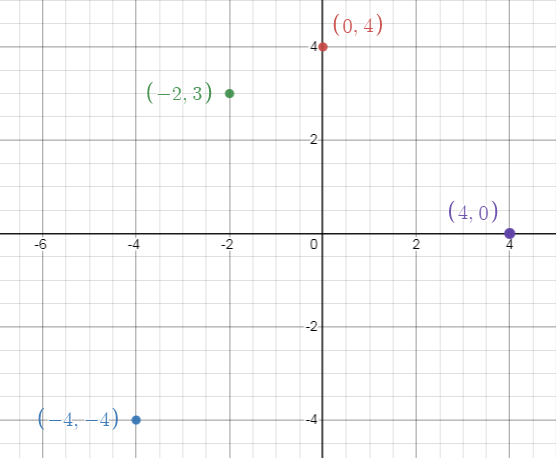
{(0, 4), (-4, -4), (-2, 3), (4, 0)}

Solution :

Table :

If x = 0 and y = 4

x = -4 and y = -4

x = -2 and y = 3

x = 4 and y = 0

Graph :

Mapping a diagram :

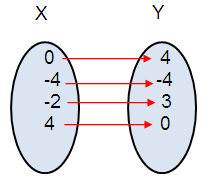
Domain :

{0, -4, -2, 4}

Range :

{-4, 0, 3, 4}