EXPRESSING NUMBERS AS A PRODUCT OF PRIME FACTORS WORKSHEET

Express the following numbers as product of prime factors.

Problem 1 :

52

Solution :

In 52, the unit digit is 2. So, it is even number. Then it is divisible by 2.

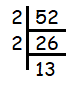
52 = 2 x 2 x 13

Here 2 is repeating two times and no more factors which are repeating.

Writing in the exponential form, we get

52 = 2² x 13

Problem 2 :

90

Solution :

The given number 90 ends with 0. Then, it must be the multiple of 2.

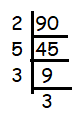
90 = 2 x 5 x 3 x 3

3 is repeating two times and no more factors are repeating. Writing in the exponential form, we get

= 2 x 5 x 3²

Problem 3 :

72

Solution :

The given number 72 ends with 2. Then, it must be the multiple of 2.

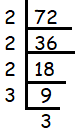
72 = 2 x 2 x 2 x 3 x 3

The factor 2 is repeating three times and the factor 3 is repeating two times. Then, writing the repeating factors in exponential form. 

= 2³ x 3²

Problem 4 :

100

Solution :

Since 100 ends with 0, it must be multiple of 2 or 5.

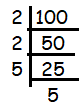
100 = 2 x 2 x 5 x 5

The factor 2 is repeating two times and the factor 5 is repeating two times. Then, writing the repeating factors in exponential form. 

100 = 2² x 5²

Problem 5 :

64

Solution :

Since 64 ends with 4, it must be multiple of 2.

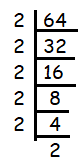
64 = 2 x 2 x 2 x 2 x 2 x 2

The factor 2 is repeating six times. Then, writing the repeating factors in exponential form. 

64 = 2⁶

Problem 6 :

105

Solution :

Since 105 ends with 5, it must be divisible by 5.

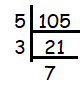
105 = 5 x 3 x 7

Since there is no repeating factor, so we cannot express it in exponential form.

Problem 7 :

120

Solution :

Since 120 ends with 0, it must be divisible by 2.

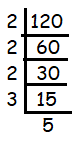
120 = 2 x 2 x 2 x 3 x 5

The factor 2 is repeating three times and no more factor is repeating. Then, writing the repeating factors in exponential form. 

120 = 2³ x 3 x 5

Problem 8 :

85

Solution :

Since 85 ends with 5, it must be divisible by 5.

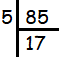
85 = 5 x 17

Problem 9 :

96

Solution :

Since 96 ends with 6, it must be divisible by 2.

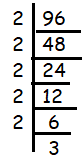
96 =  2 x 2 x 2 x 2 x 2 x 3

The factor 2 is repeating five times and no more factor is repeating. Then, writing the repeating factors in exponential form. 

96 =  2⁵ x 3

Problem 10 :

112

Solution :

Since 112 ends with 2, it must be divisible by 2.

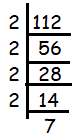
112 =  2 x 2 x 2 x 2 x 7

The factor 2 is repeating four times  and no more factor is repeating. Then, writing the repeating factors in exponential form. 

112 =  2⁴ x 7

Problem 11 :

84

Solution :

Since 84 ends with 4, it must be divisible by 2.

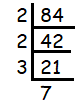
84 =  2 x 2 x 3 x 7

Since 2 is repeating 2 times and no more factors are repeating. We can write it in exponential form.

84 =  2² x 3 x 7

Problem 12 :

108

Solution :

Since 108 ends with 8, it must be divisible by 2.

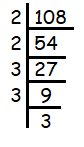
108 =  2 x 2 x 3 x 3 x 3

Since 2 is repeating 2 times and 3 is repeating three times. So, we can write in the exponential form.

108 =  2² x 3³

Problem 13 :

56

Solution :

Since 56 ends with 6, it must be divisible by 2.

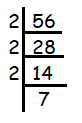
56 =  2 x 2 x 2 x 7

Since 2 is repeating 3 times and no more factor is repeating. So, we can write in the exponential form.

56 =  2³ x 7