EXPONENTS AND EXPONENTIAL FUNCTIONS

Problem 1 :

The function f(x) = 2(2)^x was replaced with f(x) + k , resulting in the function graphed below.

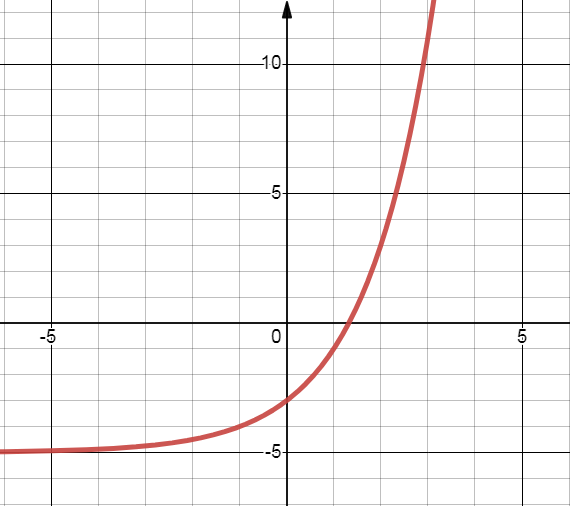
What is the value of k?

Solution:

f(x) = 2(2)^x

y-intercept: x = 0

y = 2(2)⁰

y = 2

So, the new function goes from 2 to -3. (i.e) 5 units down.

So, k = -5

Problem 2 :

Monica did an experiment to compare two methods of warming an object. The results are shown in the table below.

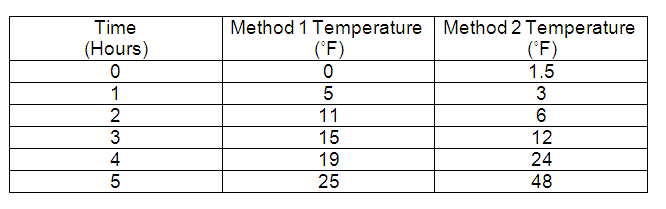
Which statements best describes her results?

A. The temperature using both methods changed at a constant rate.

B. The temperature using both methods changed exponentially.

C. The temperature using Method 2 changed at a constant rate.

D. The temperature using Method 2 changed exponentially.

Solution:

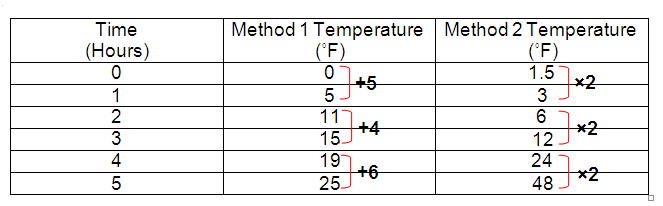
The temperature using Method 2 changed exponentially.

So, option (D) is correct.

Problem 3 :

The value of an antique car is modeled by the function V(x) = 107,000(1.009)^(2/3x) where x is the number of years since 2005. By what approximate percent rate is the value of the car increasing per year?

A. 0.04%         B. 0.14%          C. 0.60%        D. 1.40%

Solution:

So, option (C) is correct.

Problem 4 :

Solution:

So, option (B) is correct.

Problem 5 :

Solution:

So, option (D) is correct.

Problem 6 :

The value V, of a car can be modeled by the function V(t) = 13,000 (0.82)^t, where t is the number of years since the car was purchased. To the nearest tenth of a percent, what is the monthly rate of depreciation?

A. 1.5%    B. 1.6%     C. 9.2%     D. 18.0%

Solution:

V(t) = 13,000 (0.82)^t

y = a (1 - r)^t

1 - r = 0.82

-r = 0.82 - 1

-r = -0.18

r = 0.18 × 100

r = 18%

So, option (D) is correct.

Problem 7 :

The current student population of the Brentwood Student Center is 2,000. The enrollment at the center increases at a rate of 4% each year. To the nearest whole number, what will the student population be closest to in 3 years?

(1) 2,240          (2) 2,250       (3) 5,488         (4) 6,240

Solution:

Given, P = total population

r = 4% = 0.04

n = 3 years

P = 2000 (1 + r)ⁿ

= 2000 (1 + 0.04)³

= 2000 (1.04)³

= 2000 (1.124864)

P = 2249.728

Rounded to the nearest whole number, and we get

P = 2250

So, option (2) is correct.

Problem 8 :

Mr. Smith invested $2,500 in a savings savings account that earns 3% interest compounded annually. He made no additional deposits or withdrawals. Which expression can be used to determine the number of dollars in this account at the end of 4 years?

(1) 2500(1 + 0.03)⁴             (2) 2500(1 + 0.3)⁴

(3) 2500(1 + 0.04)³            (4) 2500(1 + 0.4)³

Solution:

Given, P = 2500, r = 3% = 0.03, n = 1, t = 4

So, option (1) is correct.

Problem 9 :

Solution:

So, option (B) is correct.

Problem 10 :

The table below shows the average weight of a type of plankton after several weeks.

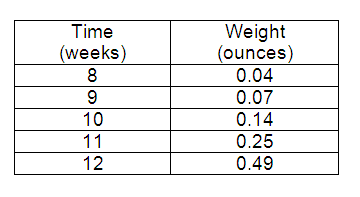
What is the average rate of change in weight of the plankton from week 8 to week 12?

A. 0.0265 ounce per week   B. 0.0375 ounce per week

C. 0.055 ounce per week      D. 0.1125 ounce per week

Solution:

Let x = Time and y = Weight 

So, option (D) is correct.

Problem 11 :

Trina has a college fund started with a  deposit of $10,000 which earns 5% annually. If no other monies are deposited, how much money will Trina have in her fund at the end of three years?

(1) $11,500       (2) $11,576.25           (3) $15,000

(4) $25,000

Solution:

Given, P = $10000

r = 5% = 0.05

t = 3 years

So, option (2) is coorect.