EXPONENTIAL GROWTH AND DECAY WORD PROBLEMS

Problem 1 :

The weight of bacteria in a culture t hours after it has been established is given by

W_t = 2.5 × 2^0.04t

grams. After what time will the weight reach

a. 4 grams     b. 15 grams

Solution:

a) Weight = 4 grams

4 = 2.5 × 2^0.04t

4/2.5 = 2^0.04t

1.6 = 2^0.04t

log 1.6 = 0.04t log 2

0.04t = log 1.6/log 2

0.04t = 0.2041/0.3010

0.04t = 0.6780

t = 0.6780/0.04

t = 16.95

Approximately 17 hours.

b)  Weight = 15 grams

15 = 2.5 × 2^0.04t

15/2.5 = 2^0.04t

6 = 2^0.04t

log 6 = 0.04t log 2

0.04t = log 6/log 2

0.04t = 0.7781/0.3010

0.04t = 2.585

t = 2.585/0.04

t = 64.62

Approximately 64.6 hours.

Problem 2 :

The population of bees in hive, t hours after it has been discovered, is given by 

P_n = 5000 x 2^0.09t

After what time the population will reach 

a. 15000    b. 50000

Solution :

a)  P_n = 5000 x 2^0.09t

15000 = 5000 x 2^0.09t

2^0.09t = 15000/5000

2^0.09t = 3

log (2^0.09t) = log 3

0.09t log 2 = log 3

0.09t = log 3 / log 2

0.09t = 0.4771/0.3010

0.09t = 1.58

t = 17.55

Approximately 17.6 hours.

b)  P_n = 5000 x 2^0.09t

50000 = 5000 x 2^0.09t

2^0.09t = 50000/5000

2^0.09t = 10

log (2^0.09t) = log 10

0.09t log 2 = 1

0.09t = 1/0.3010

t = 36.9 hours

Problem 3 :

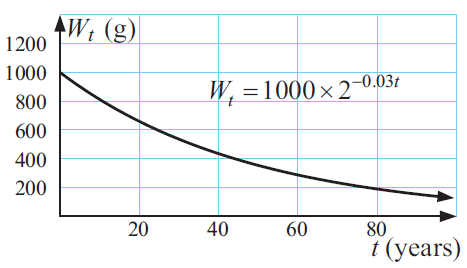
The weight W_t grams of radioactive substance remaining after t years is given by 

W_t = 1000 x 2^-0.03t grams. Find

i)  The initial weight

ii)  The weight after 

a) 10 years    ii) 100 years     iii) 1000 years

iii)  Graph W_t against t using a and b only

Solution :

W_t = 1000 x 2^-0.03t

i) Initial weight, when t = 0

W₀ = 1000 x 2^-0.03(0)

W₀ = 1000 grams

ii)  The weight after 

a) 10 years    ii) 100 years     iii) 1000 years

when t = 1000

W₁₀₀₀ = 1000 x 2^-0.03(1000)

W₁₀₀₀ = 1000 x 2^-30

W₁₀₀₀ = 1000 x 9.313 x 10^-10

W₁₀₀₀ = 10³ x 9.313 x 10^-10

W₁₀₀₀ = 9.313 x 10^-7

Problem 4 :

The weight of radioactive substance after t years is given by the formula 

W_t = W₀  x 3^-0.003t grams. Find

i)  The initial weight

ii)  The percentage remaining after

a) 100 years    ii) 500 years     iii) 1000 years

Solution :

i) Initial weight, when t = 0

W_t = W₀  x 3^-0.003(0)

W_t = W₀ grams

ii)  The weight after 

i) 100 years    ii) 500 years     iii) 1000 years

i)  when t = 100

W₁₀ = W₀ x 3^-0.003(100)

W₁₀ = W₀ x 3^-0.3

W₁₀ = W₀ x 0.719

Converting into percentage, we get

71.9 % of W₀

ii)  when t = 500

W₅₀₀ = W₀ x 3^-0.003(500)

W₅₀₀ = W₀ x 3^-1.5

W₅₀₀ = W₀ x 0.192

Converting into percentage, we get

19.2 % of W₀

iii)  when t = 1000

W₁₀₀₀ = W₀ x 3^-0.003(1000)

W₁₀₀₀ = W₀ x 3^-3

W₁₀₀₀ = W₀ x 0.03703

Converting into percentage, we get

3.7 % of W₀

Problem 5 :

The temperature T_t (°C) of a liquid which has been placed in a refrigerator is give by

T_t = 100 x 2^-0.04t

a) the initial temperature

b)  The temperature after 

i) 10 minutes     ii)  25 minutes      iii)  60 minutes

c) Find how long it takes for the temperature to reach 20°C.

Solution :

T_t = 100 x 2^-0.04t

a) Initial temperature, when t = 0

T₀ = 100 x 2^-0.04(0)

T₀ = 100

b)  The temperature after 

i) 10 minutes

T₁₀ = 100 x 2^-0.04(10)

T₁₀ = 100 x 2^-0.4

T₁₀ = 75.78

ii)  25 minutes

T₂₅ = 100 x 2^-0.04(25)

T₂₅ = 100 x 2^-1

T₂₅ = 50

iii)  60 minutes

T₆₀ = 100 x 2^-0.04(60)

T₆₀ = 100 x 2^-2.4

T₆₀ = 18.94

Problem 6 :

The weight W_t (°C) of a radioactive substance remaining after t years is given by the formula

W_t = W₀ x 2^-0.0005t

a) the original weight

b)  The weight loss after 1200 years 

Solution :

a)  W_t = W₀ x 2^-0.0005t

Original weight, when t = 0

W_t = W₀ x 2^-0.0005(0)

Initial weight is W₀

b)  The weight loss after 1200 years 

When t = 1200

W₁₂₀₀ = W₀ x 2^{-0.0005(1200)}

W₁₂₀₀ = W₀ x 0.9597