EXPONETIAL EXPRESSIONS WORD PROBLEMS

Problem 1 :

In January, the parks and Wildlife department released 267 bass into a newly constructed pond. Each month, the population of bass in the pond increases by 4.2%. At this rate of growth, what function can be used to determine the population of bass m months after January ?

Solution :

The initial amount of bass = 267

Each month the population of bass increases by 4.2%.

Initial population be 100%.

Growth rate = 100% + 4.2%

= 104.2%

= 1.042

Required exponential function :

y = 267 (1.042)^m

Problem 2 :

A pyramid at chicken Itza in Mexico contains several layers that are in the shape of square prisms. The first layer has a side of 50 meters and each successive layer has a side length that is 95% of the one directly below it. What function can be used to find the side length, in meters of layer, where 1 ≤ L ≤ 6 ?

Solution :

Initial value = 50 meter, a = 50

Side length of every layer decreases by 95%.

y = 50(0.95)^L

Here L = 1, 2, 3, 4, 5, 6

Problem 3 :

An official NBA basketball must be inflated so that when it is dropped, it must not bounce back more than 75% of he height from which it was dropped. If a basket ball is dropped from a height of 72 inches, what function r(t) describes the height of the basket ball as a function of t, the number of bounces ?

Solution :

Initial height when the basket ball is dropped (a) = 72 inches

Every time it bounce back to 75% of height from which it was dropped

Common ratio = (100 + 75)%

= 175%

b = 1.75

Number of times bouncing back = n

r(t) = 72 (1.75)^t

Problem 4 :

The population of Bexar Country Texas, for a few recent years is shown in the table.

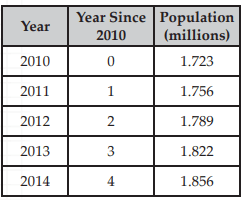
If t represents the number of years since 2010 and P(t) represents the population in millions, what function, P(t) best describes the data in the table ?

Solution :

Initial value(a) = 1.723

Check if the multiplication factor are same :

1.756/1.723 ==>  1.01

1.789/1.756 ==> 1.01

1.822/1.789 ==> 1.01

1.856/1.822 ==> 1.01

Common ratio is same, so it is exponential function.

b = 1.01

P(t) = 1.723 (1.01)^t

Problem 5 :

A chiropterologist is a scientist who studies bats. A bat colony is discovered and a chiropterologist calculates that there are 2100 bats in the colony. If the population of the colony doubles each year, which function, B(t)  describes the population of the colony t year after discovery ?

(a) B(t) = 2100(1/2)^t         (b) B(t) = 2100(2)^t

(c) B(t) = 2100 +2^t         (d) B(t) = 2100 + (1/2)^t

Solution :

Initial population(a) = 2100

In the second year, population of bats = 2(2100)

In the third year, population of bats = 2[2(2100)] => 2² (2100)

After t years, the population :

B(t) = 2^t (2100)

Problem 6 :

Chuy purchased a used truck for $11500. According to an online vehicle website, his truck will depreciate or lose value, at a rate of 5.5% each year. What function d(x) represents the value of Chuy's truck x year after its purchase ?

(a) d(x) = 11500(0.945)^x         (b) d(x) = 11500(1.055)^x

(c) d(x) = 11500(0.055)^x        (d) d(x) = 11500(5.5)^x

Solution :

Initial value a = 11500

Since the value is depreciating, common ratio = (100-5.5)%

= 94.5%

= 0.945

x be the number of years after its purchase.

d(x) = 11500 (0.945)^x