EXAMPLE OF SOLVING LOGARITHMIC INEQUALITIES
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
To solve logarithmic inequalities, we should be aware of properties of logarithm and rules followed in inequalities.
Conversion between logarithmic form to exponential form :
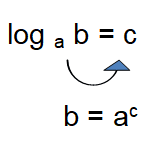
Note :
- When log y x > k, if y > 1, then x > yk
- When log y x > k, if 0 < y < 1, then x < yk
The problem can be solved using change base rule, the detailed example is given below.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Solve the inequality.
Problem 1 :
Solution :
Solution is (125, ∞).
Problem 2 :
Solution :
The solution is (0, 64]
Problem 3 :
Solution :
Solution is [4, ∞).
Problem 4 :
Solution :
Solution is [4, ∞).
Problem 5 :
Solution :
Solution is [64, ∞).
Problem 6 :
Solution :
Solution is [81, ∞).
Problem 7 :
Solution :
Solution is (0, 108)
Problem 8 :
|
10x + 3 > 0 10x > -3 x > -3/10 |
7x - 4 > 0 7x > 4 x > 4/7 |
- Considering x > -7/3, all negative values should be ignored. The possible solution is (0, ∞).
- Considering x > -3/10, all negative values should be ignored. The possible solution is (0, ∞).
- Considering x > 4/7, the possible solution is (4/7, ∞).
By considering all three, the solution for the given inequality should be (4/7, ∞).
Problem 9 :
log x + log (2 - x) < 1
Solution :
log x + log(2 - x) < 1
log [x(2 - x)] < 1
Moving base to the other side of the inequality sign, we get
x(2 -x) < 101
2x - x2 < 10
-x2 + 2x - 10 < 0
x2 - 2x + 10 > 0
This quadratic inequality cannot be solved using the method of factoring.
a = 1, b = -2 and c = 10
b2 - 4ac = (-2)2 - 4(1)(10)
= 4 - 40
= -36 < 0
Domain is (0, 2). So, the solution is (0, 2).
Problem 10 :
Solution :
Domain of log2 (x2 - x - 6)
x2 - x - 6 > 0
(x - 3) (x + 2) > 0
x > 3 and x > -2
Domain of the function is (-2, ∞) u (3, ∞), solution by solving the logarithmic inequality is (-∞, 7).
By considering all these three, we get the solution as (3, 7).
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling