EVEN AND ODD FUNCTIONS GRAPHS AND TABLES
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
A Function can be classified as Even, Odd or Neither. This classification can be determined graphically or algebraically.
How to check if the graph is odd ?
The graph will be symmetric with respect to the origin.
In other words :
If you spin the picture upside down about the Origin, the graph looks the same!
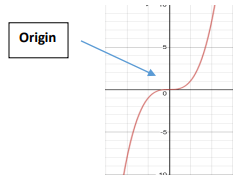
How to check if the graph is even ?
The graph will be symmetric with respect to the y-axis.
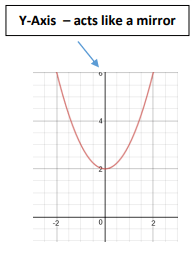
Properties of odd and even functions :
Properties of odd function :
- The graph is symmetric about origin.
- The exponents of all terms in its equation are odd.
Properties of even function :
- The graph is symmetric about y-axis.
- The exponents of all terms in its equation are even.
Problem 1 :
Which function is an even function?
a. y = h(x) = √x b. y = p(x) = x3
c. y = R(x) = 1/x d. y = |x|
Solution :
Option a :
y = h(x) = √x
Put x = -x
h(-x) = √-x
The function is not defined for negative values
Option b :
y = p(x) = x3
Put x = -x
p(-x) = (-x)3
p(-x) = -x3
It is odd function.
Option c :
y = R(x) = 1/x
Put x = -x
R(-x) = 1/(-x) ==> -1/x
R(-x) = -1/x
It is odd function.
Option d :
y = |x|
Put x = -x
y = |-x|
y = x
that is, f(-x) = f(x). It is even function.
Problem 2 :
Examine these functions. Which statement is correct?
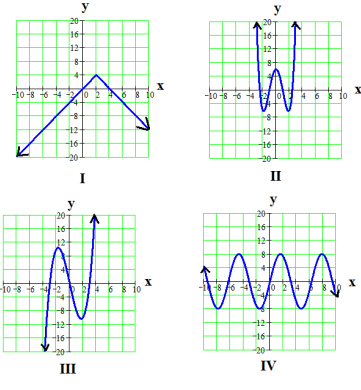
a. Graph I is the graph of an even function.
b. Graph II is symmetric to the x-axis.
c. Graph III is symmetric to the y-axis.
d. Graph IV is an odd function.
Solution :
Option a :
Graph I is the graph of an even function.
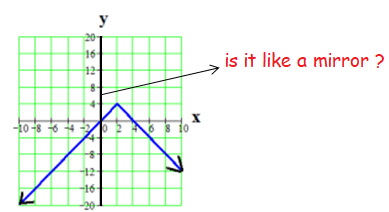
Option b :
Graph II is symmetric to the x-axis.
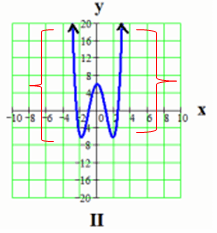
Here the y-axis is like a mirror.
Option c :
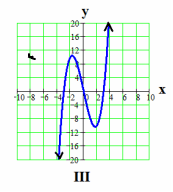
It is symmetric about origin. But option c says, it is symmetric to the y-axis. So, it is incorrect.
Option d :
It is symmetric about origin. So, option d is correct.
Problem 3 :
Which function could be an even function?
a) A function known as d(x) where d(3) = 10 and d (-3) = -10
b) A function known as k(x) where k(7) = 20 and k(-7) = 20
c) A function known as M(x) where M(4) = 10 and M (-4) = 0
d) A function known as C(x) where C(7) = - 6 and C(-7) = 6
Solution :
Even function will be symmetric about y-axis.
All points that lie on the curve will be on the rule given below,
(x, y) ==> (-x, y)
Option a :
d(3) = 10 and d (-3) = -10
When x = 3, y = 10
when x = -3, y = -10
It does not satisfy the rule above. So, it is not symmetric about y-axis and it is not even.
Option b :
k(7) = 20 and k(-7) = 20
When x = 7, y = 20
when x = -7, y = 20
It satisfies the above rule. So, it is even function.
Problem 4 :
Start with the incomplete graph of p(x) as shown. Complete the graph if p(x) is symmetric to the origin
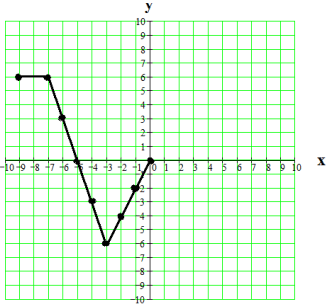
Solution :
Even function will be symmetric about origin.
All points lie on the curve will follow the rule given below.
(x, y) ==> (-x, -y)
Before the rule
|
After the rule
|
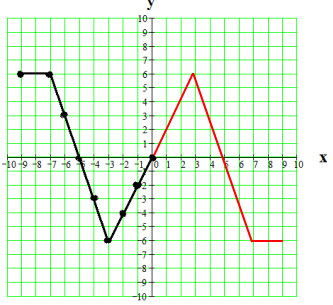
Problem 5 :
Start with the incomplete graph of f(x) as shown. Complete the graph if f(x) is symmetric to the y-axis.

Solution :
Even function will be symmetric about y-axis.
All points lie on the curve will follow the rule given below.
(x, y) ==> (-x, y)
|
|
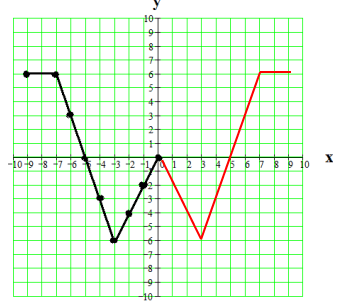
Problem 6 :
If g(x) is an odd function and g(5) = -7, which one of the following must be true?
a. g(-5) = 7 b. g(-5) = -7 c. g(-7) = 5 d. g(7) = - 5
Solution :
Odd function is symmetric about origin. The points that lie on the curve will follow the rule below.
(x, y) ==> (-x, -y)
If g(5) = -7, the g(-5) = 7
Option a is correct.
Problem 8 :
Which function is not even (symmetric to the y-axis)?
a. y = -4 x2 + 3 b. y = 2 |x| - 6
c. y = x2 +6x + 5 d. y = 6
Solution :
If the function satisfies the condition, f(-x) = f(x), then it is even function.
Option a :
f(x) = -4 x2 + 3
f(-x) = -4 (-x)2 + 3
f(-x) = -4 x2 + 3
f(-x) = f(x)
It is even
Option b :
f(x) = 2 |x| - 6
Put x = -x
f(-x) = 2|-x| - 6
f(-x) = 2|x| - 6
f(-x) = f(x)
So, it is even.
Option c :
f(x) = x2 +6x + 5
f(-x) = (-x)2 + 6(-x) + 5
f(-x) = x2 - 6x + 5
f(-x) ≠ f(x)
It is not even. So, option c is correct.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling