EVALUATING WITH OPERATIONS ON FUNCTIONS

Problem 1 :

Compute (f + g)(2), (f - g)(-1), (fg)(1/2), and (f/g)(0).

(a) f(x) = x² - x, g(x) = 12 - x²

(b) f(x) = √(x + 3), g(x) = 2x - 1

Solution:

(a)

(f + g)(2) :

(f + g)(2) = f(2) + g(2)

f(2) = 2² - 2

= 2

g(2) = 12 - 2²

= 8

f(2) + g(2) = 2 + 8

= 10

(f - g)(-1) :

(f - g)(-1) = f(-1) - g(-1)

f(-1) = (-1)² - (-1)

= 2

g(-1) = 12 - (-1)²

= 11

f(-1) - g(-1) = 2 - 11

= -9

(fg)(1/2) :

(fg)(1/2) = f(1/2) ⋅ g(1/2)

f(1/2) = (1/2)^{2 -} (1/2)

= -1/4

g(1/2) = 12 - (1/2)²

= 47/4

(f/g)(0) :

(f/g)(0) = f(0)/g(0)

f(0) = 0 - 0

= 0

g(0) = 12 - 0

= 12

(b) 

(f + g)(2) :

(f + g)(2) = f(2) + g(2)

f(2) = √(2 + 3)

= √5

g(2) = 2(2) - 1

= 3

f(2) + g(2) = √5 + 3

(f - g)(-1) : 

(f - g)(-1) = f(-1) - g(-1)

f(-1) = √(-1 + 3)

= √2

g(-1) = 2(-1) - 1

= -3

f(-1) - g(-1) = √2 + 3

(fg)(1/2) :

(fg)(1/2) = f(1/2) ⋅ g(1/2)

f(1/2) = √(1/2 + 3)

= √7/2

g(1/2) = 2(1/2) - 1

= 0

f(1/2) ⋅ g(1/2) = √7/2 ⋅ 0

= 0

(f/g)(0) :

(f/g)(0) = f(0)/g(0)

f(0) = √(0 + 3)

= √3

g(0) = 2(0) - 1

= -1

(c)

(f + g)(2) :

(f + g)(2) = f(2) + g(2)

f(2) = 2(2)

= 4

(f - g)(-1) :

(f - g)(-1) = f(-1) - g(-1)

f(-1) = 2(-1)

= -2

f(-1) - g(-1) = -2 + 1

= -1

(fg)(1/2) :

(fg)(1/2) = f(1/2) ⋅ g(1/2)

f(1/2) = 2(1/2)

= 1

(f/g)(0) :

(f/g)(0) = f(0)/g(0)

f(0) = 2(0)

= 0

(d)

(f + g)(2) :

(f + g)(2) = f(2) + g(2)

f(2) = 2²

= 4

g(2) = 1/2²

= 1/4

f(2) + g(2) = 4 + 1/4

= 17/4

(f - g)(-1) :

(f - g)(-1) = f(-1) - g(-1)

f(-1) = (-1)²

= 1

g(-1) = 1/(-1)²

= 1

(fg)(1/2) :

(fg)(1/2) = f(1/2) g(1/2)

f(1/2) = (1/2)²

= 1/4

f(1/2) g(1/2) = 1/4(4)

= 1

(f/g)(0) :

(f/g)(0) = f(0)/g(0)

f(0) = 0

g(0) = undefined

f(0)/g(0) = 0/undefined

= undefined

Problem 2 :

Use the table to state the domain of f(x) and g(x). Then find the following:

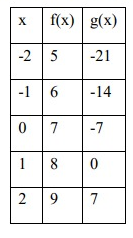
a. (f + g)(1)

b. (f/g)(0)

c. (f/g)(1)

d. f(-2) - g(2)

e. (2g + f)(-1)

Solution:

a. 

(f + g)(1) = f(1) + g(1)

= 8 + 0

= 8

b.

(f/g)(0) = f(0)/g(0)

= 7/-7

= -1

c.

(f/g)(1) = f(1)/g(1)

= 8/0

= undefined

d.

= f(-2) - g(2)

= 5 - 7

= -2

e.

(2g + f)(-1) = 2g(-1) + f(-1)

= 2(-14) + 6

= -28 + 6

= -22

Problem 3 :

Let f(x) = x² + 7x + 12 and g(x) = x² - 9. State the domain if there are any restrictions.

a) Find (f + g)(x)

b) Find (2f - 3g)(x)

c) Find (fg)(x)

d) Find (f/g)(-2)

Solution:

a) 

(f + g)(x) = f(x) + g(x)

= x² + 7x + 12 + x² - 9

= 2x² + 7x + 3

= (2x + 1)(x + 3)

b) 

(2f - 3g)(x) = 2f(x) - 3g(x)

= 2(x² + 7x + 12) - 3(x² - 9)

= 2x² + 14x + 24 - 3x² + 27

= -x² + 14x + 51

= -(x - 17)(x + 3)

c)

(fg)(x) = f(x) g(x)

= (x² + 7x + 12)(x² - 9)

= x⁴ + 7x³ + 21x² + 63x + 108

d) 

(f/g)(-2) = f(-2)/g(-2)

f(-2) = (-2)² + 7(-2) + 12

= 4 - 14 + 12

= 2

g(-2) = (-2)² - 9

= 4 - 9

= -5

Problem 4 :

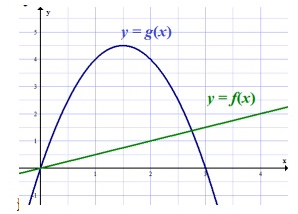
Use the graph to state the domain of f(x) and g(x). Then find the following.

a) (f + g)(1)

b) (fg)(1)

c) f(4) - g(2)

d) (2g + f)(3)

Solution:

a)

(f + g)(1) = f(1) + g(1)

= 0.5 + 4

= 4.5

b)

(fg)(1) = f(1) g(1)

= (0.5)(4)

= 2

c)

= f(4) - g(2) 

= 2 - 4

= -2

d)

(2g + f)(3) = 2g(3) + f(3)

= 2(0) + 1.5

= 1.5