EVALUATING TRIGONOMETRIC FUNCTIONS GIVEN A POINT ON THE TERMINAL SIDE

The coordinates of a point P on the terminal arm of each angle are shown. Write the exact trigonometric ratios sin θ, cos θ, and tan θ for each.

Problem 1 :

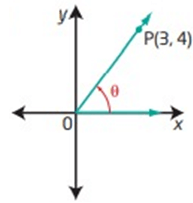
Solution :

By drawing a perpendicular line from P to the x-axis, we will get a right triangle. Then OP be the hypotenuse.

Use the Pythagorean Theorem,

sin θ = Opposite side / Hypotenuse

sin θ = 4/5

cos θ = Adjacent side / Hypotenuse

cos θ = 3/5

tan θ = Opposite side / Adjacent side

tan θ = 4/3

Problem 2 :

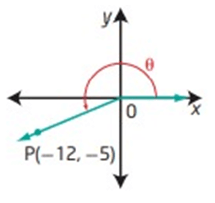
Solution :

By drawing a perpendicular line from P to the x-axis, we will get a right triangle. Then OP be the hypotenuse.

sin θ = Opposite side / Hypotenuse

sin θ = -5/13

cos θ = Adjacent side / Hypotenuse

cos θ = -12/13

tan θ = Opposite side / Adjacent side

tan θ = -5/-12

tan θ = 5/12

Problem 3 :

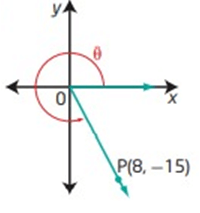
Solution :

By drawing a perpendicular line from P to the x-axis, we will get a right triangle. Then OP be the hypotenuse.

sin θ = Opposite side / Hypotenuse

sin θ = -15/17

cos θ = Adjacent side / Hypotenuse

cos θ = 8/17

tan θ = Opposite side / Adjacent side

tan θ = -15/8

Problem 4 :

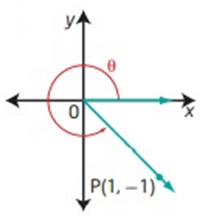
Solution :

sin θ = Opposite side / Hypotenuse

sin θ = -1/√2

sin θ = -√2/2

cos θ = Adjacent side / Hypotenuse

cos θ = 1/√2

cos θ = √2/2

tan θ = Opposite side / Adjacent side

tan θ = -1/1

tan θ = -1

Determine the exact of sin θ, cos θ, and tan θ if the terminal arm of an angle in standard position passes through the given point.

Problem 5 :

P (-5, 12)

Solution :

Since the given point is in the form of (-x, y), it will be in second quadrant.

Accordingly ASTC, for the trigonometric ratios sin θ and cosec θ alone we have positive.

sin θ = Opposite side / Hypotenuse

sin θ = 12/13

cos θ = Adjacent side / Hypotenuse side

cos θ = -5/13

tan θ = Opposite side / Adjacent side

tan θ = -12/5

Problem 6 :

P (5, -3)

Solution :

Since the given point is in the form of (x, -y), it will be in fourth quadrant.

Accordingly ASTC, for the trigonometric ratios cos θ and sec θ alone we have positive.

sin θ = Opposite side / Hypotenuse side

sin θ = -3/√34

cos θ = Adjacent side / Hypotenuse side

cos θ = 5/√34

tan θ = Opposite side / Adjacent side

tan θ = -3/5

Problem 7 :

P (6, 3)

Solution :

Since the given point is in the form of (x, y), it will be in fourth quadrant.

Accordingly ASTC, for all trigonometric ratios we have to use positive sign.

sin θ = Opposite side / Hypotenuse

sin θ = 3√5

= 1/√5

sin θ = 1/√5

cos θ = Adjacent side / Hypotenuse

cos θ = 6/ 3√5

cos θ = 2/√5

tan θ = Opposite side / Adjacent side

tan θ = 3/6

tan θ = 1/2

Problem 8 :

P (-24, -10)

Solution :

Since the given point is in the form of (-x, -y), it will be in third quadrant.

Accordingly ASTC, for the trigonometric ratios tan θ and cot  θ alone we have positive.

sin θ = Opposite side / Hypotenuse

sin θ = -10/26

sin θ = -5/13

cos θ = Adjacent side / Hypotenuse

cos θ = -24/26

cos θ = -12/13

tan θ = Opposite side / Adjacent side

tan θ = -10/-24

tan θ = 5/12