EVALUATING TRIGONOMETRIC EXPRESSIONS

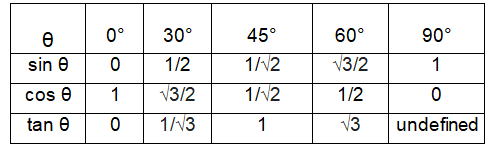
Here we will see how we evaluate trigonometric expressions.

The table will be very helpful, when evaluating trigonometric functions.

Converting radian to degree :

π = 180 π/2 = 90 π/3 = 60 π/4 = 45 π/6 = 30

3π/2 = 270 5π/4 = 225 2π/3 = 120

If the angle measure is more than 180 degree, then using ASTC formula, we can find the value of given trigonometric function.

Without using a calculator, evaluate:

Problem 1 :

sin² 60˚

Solution :

sin² 60˚ = (√3/2)²

sin² 60˚ = 3/4

Problem 2 :

sin 30˚ cos 60˚

Solution :

sin 30˚ cos 60˚ = (1/2) (1/2)

sin 30˚ cos 60˚ = 1/4

Problem 3 :

4sin 60˚ cos 30˚

Solution :

4sin 60˚ cos 30˚ = 4(√3/2) (√3/2)

= 4(3/4)

4sin 60˚ cos 30˚ = 3

Problem 4 :

1 - cos² (π/6)

Solution :

1 - cos² (π/6) = 1 - (√3/2)²

= 1 - 3/4

1 - cos² (π/6) = 1/4

Problem 5 :

sin² (2π/3) - 1

Solution :

= sin² (2π/3) - 1

sin 2π/3 = sin 120

= sin (90 + 30)

= cos 30

sin 2π/3 =  √3/2

sin² (2π/3) - 1 = (√3/2)² - 1

= 3/4 - 1

sin² (2π/3) - 1 = -1/4

Problem 6 :

cos² (π/4) - sin (7π/6)

Solution :

cos² (π/4) - sin (7π/6) = (1/√2)² - (-1/2)

= 1/2 + 1/2

cos² (π/4) - sin (7π/6) = 1

Problem 7 :

sin (3π/4) - cos (5π/4)

Solution :

sin (3π/4) - cos (5π/4) = (1/√2) - (-1/√2)

= 1/√2 + 1/√2

sin (3π/4) - cos (5π/4) = √2

Problem 8 :

1 - 2 sin² (7π/6)

Solution :

sin 7π/6 = sin 210

= sin (180 + 30)

= -sin 30

= -1/2

1 - 2 sin² (7π/6) = 1 - 2(-1/2)²

= 1 - 2(1/4)

1 - 2 sin² (7π/6) = 1/2

Problem 9 :

cos² (5π/6) - sin² (5π/6)

Solution :

cos² (5π/6) - sin² (5π/6) = (-√3/2)² - (1/2)²

= 3/4 - 1/4

cos² (5π/6) - sin² (5π/6) = 1/2

Problem 10 :

tan² (π/3) - 2sin² (π/4)

Solution :

tan π/3 = tan 60 = √3

sin π/4 = sin 45 = 1/√2

tan² (π/3) - 2sin² (π/4) = (√3)² - 2(1/√2)²

= 2 - 2(1/2)

tan² (π/3) - 2sin² (π/4) = 2

Problem 11 :

2 tan (-5π/4) - sin (3π/2)

Solution :

tan (-5π/4) - sin (3π/2) = 2(-1) - (-1)

= -2 + 1

2tan (-5π/4) - sin (3π/2) = -1

Problem 12 :

2tan 150˚ / (1 - tan² 150˚)

Solution :

tan 150˚= tan (90 + 60)

= -cot 60

= -1/tan 60

= -1/√3

2tan 150˚ / 1 - tan² 150˚ = 2(-1/√3) / 1 - (-1/√3)²

= -2/√3 / 1 - (1/3)

= -2/√3 / 2/3

= (-2/√3) (3/2)

= -3/√3

2tan 150˚ / 1 - tan² 150˚ = -√3