EVALUATING PIECEWISE FUNCTIONS

Problem 1 :

Evaluate the following.

(a)  18    (b)  17     (c)  14     (d)  20

Solution :

To evaluate f(3), let us observe the functions.

The function will work only if the value of x is lesser than 2.

The function will work only if the value of x is greater than or equal to 2.

f(x) = 5x + 2

f(3) = 5(3) + 2

f(3) = 15 + 2

f(3) = 17

Problem 2 :

Evaluate for the given value.

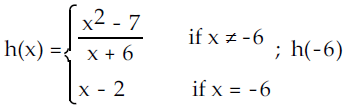
(a)  -8    (b)  undefined     (c)  8     (d)  -4

Solution :

To evaluate h(-6), let us observe the functions.

The 1^st function will work only if the value of x is not equal to -6

The 2^nd function will work only if the value of x is equal to -6.

h(x) = x - 2

h(-6) = -6 - 2

h(-6) = -8

Problem 3 :

Evaluate for the given value.

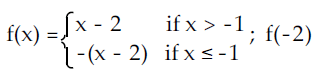
(a)  -2    (b)  17    (c)  4     (d)  -4

Solution :

To evaluate f(-2), let us observe the functions.

When x = -2, which is lesser than -1. So, we choose the second function.

f(x) = -(x - 2)

f(-2) = -(-2-2)

f(-2) = 4

Problem 4 :

Evaluate for the given value.

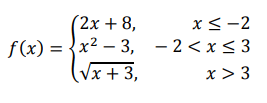
(i)  f(-4)     (ii)  f(6)      (iii)  f(-2)      (iv)  f(0)

Solution :

Problem 5 :

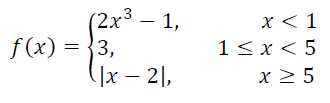
(i) f(8)      (ii)  f(0)       (iii)  f(4)       (iv)  f(5)

Solution :

Problem 6 :

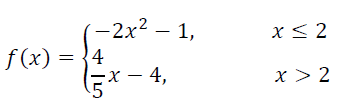
(i) f(0)      (ii)  f(5)       (iii)  f(2)       (iv)  f(-3)

Solution :

Problem 7 :

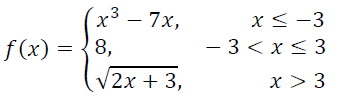
(i) f(-5)      (ii)  f(11)       (iii)  f(0)       (iv)  f(3)

Solution :

Problem 8 :

On a trip, the total distance (in miles) you travel in x hours is represented by the piecewise function

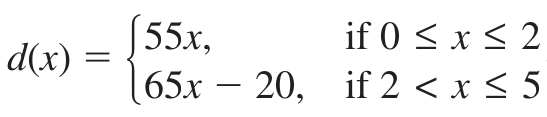
a. Interpret the domain and range of the function.

b. How far do you travel in 4 hours?

c. Compare the first 2 hours of the trip to the last 3 hours by calculating and interpreting the average rates of change.

Solution :

a.

The travelling time is in between 0 to 5 hours. So, domain is [0, 5]

Minimum distance covered = 55(0)

= 0 miles

Maximum distance covered = 65 x - 20

= 65(5) - 20

= 315 - 20

= 295 miles

So, the range is [0, 295]

b. Distance travelled in 4 hours

= 65(4) - 20

= 260 - 20

= 240 miles

c.

Distance covered in first two hours can be calculated by applying x = 2 in the first function.

Distance covered = 55(2)

= 110 miles

Distance covered in last two hours can be calculated by applying x = 3 in the second function.

= 65 (3) - 20

= 195 - 20

= 175 miles

Problem 9 :

Describe and correct the error in graphing

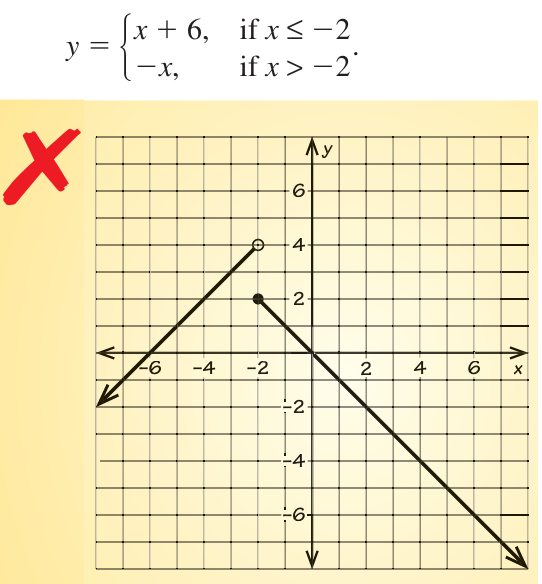
Solution :

First piece:

f(x) = x + 6

(-2, 4) (-3, 3) (-4, 2) and (-6, 0).

Second piece:

f(x) = -x

(-1, 1) (0, 0) (1, -1) and (2, -2)

By observing the graph the input -2 is not valid for the function f(x) = -x, then there should not be a solid circle, there must be a transparent circle. The solid circle and transparent circle to be switched.