EVALUATING FUNCTIONS

Problem 1 :

If f(x) = 2x−5, then what is the value of f(2) + f(5) ?

(A) 1    (B) 2    (C) 3    (D) 4      (E) 5

Solution :

f(x) = 2x−5

f(2) + f(5) :

f(2) + f(5) = -1 + 5 ==> 4

Problem 2 :

If h(x) = 3x + 5 and h(a) = 27, then what is the value of a ?

Solution :

h(a) = 27

h(x) = 3x + 5

h(a) = 3a + 5

3a + 5 = 27

Solving for a, we get

3x = 27 - 5

3a = 22

a= 22/3

Problem 3 :

Let f(x) = 4x − 3. If f(a) = 9 and f(b) = 5, then what is f(a + b) ?

(A) 5      (B) 7     (C) 14        (D) 16       (E) 17

Solution :

f(x) = 4x − 3. If f(a) = 9 and f(b) = 5

f(a) = 9 

4a - 3 = 9   -----(1)

Solving for a from (1), we get

4a = 12

a = 12/4 ==> a = 3

f(b) = 5

4b - 3 = 5 ------(2)

Solving for b from (2), we get

4b = 5 + 3

4b = 8

b = 2

f(a + b) = f(3 + 2) ==> f(5)

f(5) = 4(5) - 3

f(5) = 20 - 3

f(5) = 17

Problem 4 :

If f(x) = x² − 1, and f(2a) = 35, then what could be the value of a ?

(A) −6      (B) −3     (C) 1     (D) 2       (E) 6

Solution :

f(x) = x² − 1, and f(2a) = 35

f(2a) = (2a)² - 1

4a² - 1 = 35

4a² = 36

a² = 36/4

a² = 9

a = 3 and -3

Accordingly the options, -3 is the answer.

Problem 5 :

If f(x) = 2x+ 4, then what is the value of f(4) + f(6) ?

(A) f(8)      (B) f(10)       (C) f(12)      (D) f(18)      (E) f(28)

Solution :

f(4) = 2(4) + 4 ==> 8 + 4 ==> 12

f(6) = 2(6) + 4 ==> 12 + 4 ==> 16

f(4) + f(6) = 12 + 16

f(4) + f(6) = 28

f(12) = 2(12) + 4

f(12) = 24 + 4

f(12) = 28

Problem 6 :

z(q) = 4q + 1/2

The zoomster function z used in space flight engineering is defined above. If, for some number u, z(u + 1/2) = 1/2, then what is the value of u ?

(A) −3/2       (B) −1/2      (C) −1/8      (D) 1/8    (E) 1/2  

Solution :

Given :

z(q) = 4q + 1/2

z(u + 1/2) = 1/2

4(u + 1/2) + 1/2 = 1/2

4(u + 1 /2) = 0

u + 1/2 = 0 

u = -1/2

Problem 7 :

For the function f graphed in the xy plane above, if f(−2.5) = k, then what is f(2k) ?

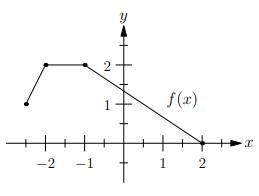
Solution :

f(−2.5) = k

By observing the graph, f(−2.5) = 1

So, k = 1, then 2k = 2

f(2) = 0

Problem 8 :

The volume of a balloon is given by the equation

V = t² - 3t + 3

What is the volume of the balloon after 3 seconds ?

(A) 3       (B) 6      (C) 9      (D) 12

Solution :

V = t² - 3t + 3

V - Volume, t - time in seconds

t = 3

V = 3² - 3(3) + 3

V = 9 - 9 + 3

V = 3

Problem 9 :

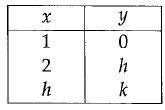
In the table above, if y = x² + x - 2, what is the value of k ?

Solution :

y = x² + x - 2

When x = 1, then y = 0

if x = 2, then y = h

h = 2² + 2 - 2

h = 4

When x = 4, y = k

k = 4² + 4 - 2

k = 16 + 4 - 2

k = 20 - 2

k = 18

Problem 10 :

The distance d, in meters, traveled by a rocket depends on the amount of fuel f, in liters, it burns according to the equation d = (2/3)f . Based on the table above, how many rockets traveled more than 20 meters ?

(A) one       (B) Two      (C) Three      (D) Four

Solution :

d = (2/3)f

Number of rockets traveled more than 20 meters = 4