EVALUATING EXPRESSIONS WITH NEGATIVE EXPONENTS

To evaluate an expression with exponents, we should to be aware of the rules of exponents. 

The Required Rules of Exponents are below.

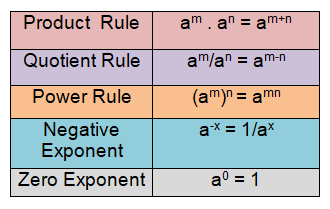
Example 1 :

yx^1/3 ⋅ xy^3/2

Solution :

= yx^1/3 ⋅ xy^3/2

By writing each term separately, we get

= y ⋅ x^1/3 ⋅ x ⋅ y^3/2

By combining the like terms, we get

= x^1/3 ⋅ x ⋅ y^3/2 ⋅ y

By using the product rule a^m ⋅ aⁿ = a^m+n, we get

= x^1/3+1 ⋅ y^3/2+1

= x^4/3 ⋅ y^5/2

So, the answer is x^4/3 ⋅ y^5/2

Example 2 :

4v^2/3 ⋅ v^-1

Solution :

= 4v^2/3 ⋅ v^-1

By writing each term separately, we get

= 4 ⋅ v^2/3 ⋅ v^-1

By using the product rule a^m ⋅ aⁿ = a^m+n, we get

= 4 ⋅ v^{2/3 - 1}

= 4v^-1/3

By using the negative exponent a^-x = 1/a^x

= (4)/v^1/3

So, the answer is (4)/v^1/3.

Example 3 :

(a^1/2 b^1/2)^-1

Solution :

= (a^1/2 b^1/2)^-1

By using the negative exponent a^-x = 1/a^x

= 1/(a^1/2 b^1/2)

So, the answer is 1/(a^1/2 b^1/2).

Example 4 :

(x⁰y^1/3)^3/2 x⁰

Solution :

= (x⁰y^1/3)^3/2 x⁰

By using the zero exponent a⁰ = 1, we get

= (1y^1/3)^3/2 1

=  (y^1/3)^3/2

By using the power rule (a^m)ⁿ = a^mn, we get

= y^{(1/3 ⋅ 3/2)}

= y^3/6

= y^1/2

So, the answer is y^1/2.

Example 5 :

(2x^1/2y^1/3)/(2x^4/3y^-7/4)

Solution :

= (2x^1/2y^1/3)/(2x^4/3y^-7/4)

By writing each term separately, we get

= x^1/2 ⋅ y^1/3 ⋅ 1/x^4/3 ⋅ 1/y^-7/4

By combining the like terms, we get

= x^1/2 ⋅ 1/x^4/3 ⋅ y^1/3 ⋅ 1/y^-7/4 

By using the quotient rule a^m/aⁿ = a^m-n, we get

= x^1/2-4/3 ⋅ y^1/3+7/4

= x^-5/6⋅ y^25/12

By using the negative exponent a^-x = 1/a^x

= y^25/12 ⋅ 1/x^5/6

= y^25/12/x^5/6

So, the answer is y^25/12/x^5/6.

Example 6 :

u^-5/4v² ⋅ (u^3/2)^-3/2

Solution :

= u^-5/4v² ⋅ (u^3/2)^-3/2

= u^-5/4 ⋅ v² ⋅ (u^3/2)^-3/2

By using the power rule (a^m)ⁿ = a^mn, we get

=  u^-5/4 ⋅ v² ⋅ u^{(3/2 ⋅ (-3/2))}

=  u^-5/4 ⋅ v² ⋅ u^-9/4

By combining the like terms, we get

=  u^-5/4 ⋅ u^-9/4 ⋅ v²

By using the product rule a^m ⋅ aⁿ = a^m+n, we get

= u^-5/4-9/4 ⋅ v²

= u^-14/4 ⋅ v²

= u^-7/2 ⋅ v²

By using the negative exponent a^-x = 1/a^x

= 1/u^7/2 ⋅ v²

= v²/u^7/2

So, the answer is  v²/u^7/2.

Example 7 :

uv ⋅ u ⋅ (v^3/2)³

Solution :

= uv ⋅ u ⋅ (v^3/2)³

= u ⋅ v ⋅ u ⋅ (v^3/2)³

By using the power rule (a^m)ⁿ = a^mn, we get

= u ⋅ v ⋅ u ⋅ v^9/2

By combining the like terms, we get

= u ⋅ u ⋅ v ⋅ v^9/2

By using the product rule a^m ⋅ aⁿ = a^m+n, we get

= u¹⁺¹ ⋅ v^1+9/2

= u² ⋅ v^11/2

So, the answer is u² ⋅ v^11/2.

Example 8 :

(2x^-2y^5/3)/x^-5/4y^-5/3 ⋅ xy^1/2

Solution :

= (2x^-2y^5/3)/x^-5/4y^-5/3 ⋅ xy^1/2

By writing each term separately, we get

= 2 ⋅ x^-2y^5/3 ⋅ 1/x^-5/4 ⋅ 1/y^-5/3 ⋅ 1/xy^1/2

By using the negative exponent 1/a^-x = a^x, we get

= 2 ⋅ x^-2y^5/3 ⋅ x^5/4 ⋅ y^5/3 ⋅ 1/xy^1/2

By using the negative exponent 1/a^x = a^-x, we get

= 2 ⋅ x^-2y^5/3 ⋅ x^5/4 ⋅ y^5/3 ⋅ x^-1 ⋅ y^-1/2

By combining the like terms, we get

= 2 ⋅ x^-2 ⋅ x^5/4 ⋅ x^-1 ⋅ y^5/3 ⋅  y^5/3 ⋅ y^-1/2

By using the product rule a^m ⋅ aⁿ = a^m+n, we get

= 2 ⋅ x^-2+5/4 ⋅ x^-1 ⋅ y^5/3+5/3 ⋅ y^-1/2

= 2 ⋅ x^-3/4 ⋅ x^-1 ⋅ y^10/3 ⋅ y^-1/2

By using the product rule a^m ⋅ aⁿ = a^m+n, we get

= 2 ⋅ x^-3/4-1 ⋅ y^10/3-1/2

= 2 ⋅ x^-7/4 ⋅ y^17/6

By using the negative exponent a^-x = 1/a^x

= 2 ⋅ y^17/6 ⋅ 1/x^7/4

= (2y^17/6)/x^7/4

So, the answer is (2y^17/6)/x^7/4.

Example 9 :

(a^3/4b^-1 ⋅ b^7/4)/3b^-1

Solution :

= (a^3/4b^-1 ⋅ b^7/4)/3b^-1

By writing each term separately, we get

= a^3/4 ⋅ b^-1 ⋅ b^7/4 ⋅ 1/3 ⋅ b^-1

By using the negative exponent 1/a^-x = a^x, we get

=  a^3/4 ⋅ b^-1 ⋅ b^7/4 ⋅ 1/3 ⋅ b

By using the product rule a^m ⋅ aⁿ = a^m+n, we get

=  a^3/4 ⋅ b^-1+7/4 ⋅ 1/3 ⋅ b

= a^3/4 ⋅ b^3/4 ⋅ b ⋅ 1/3

= a^3/4 ⋅ b^3/4+1 ⋅ 1/3

=  a^3/4 ⋅ b^7/4 ⋅ 1/3

= (a^3/4b^7/4)/3

So, the answer is (a^3/4b^7/4)/3.

Example 10 :

(3y^-5/4)/y^-1 ⋅ 2y^-1/3

Solution :

= (3y^-5/4)/y^-1 ⋅ 2y^-1/3

By writing each term separately, we get

= 3 ⋅ y^-5/4 ⋅ 1/y^-1 ⋅ 1/2 ⋅ 1/y^-1/3

By using the negative exponent 1/a^-x = a^x, we get

= 3 ⋅ y^-5/4 ⋅ y¹ ⋅ 1/2 ⋅ y^1/3

By using the product rule a^m ⋅ aⁿ = a^m+n, we get

= 3 ⋅ y^-5/4+1 ⋅ 1/2 ⋅ y^1/3

= 3 ⋅ y^-1/4 ⋅ y^1/3 ⋅ 1/2

= 3 ⋅ y^-1/4+1/3 ⋅ 1/2

= 3 ⋅ y^1/12 ⋅ 1/2

= (3y^1/12)/2

So, the answer is  (3y^1/12)/2.

Example 11 :

If x^3/5 = m and y^-3/5 = n^-1, which of the following is equal to xy ?

a)  (mn)^3/5      b)  (mn)^9/25        c)  m^5/3 n^-5/3    d)  (mn)^5/3       e) n/m

Solution :

x^3/5 = m and y^-3/5 = n^-1

x = m^5/3 ---------(1)

y = (n^-1)^-5/3

y = n^5/3 ---------(2)

xy = m^5/3 [n^5/3]

xy = (mn)^5/3

Example 12 :

x⁴ x⁶/x⁸ = 81

According to the equation above, which of the following could equal to x² ?

a)  81     b)  72      c)  18    d)  9     e)  3

Solution :

x⁴ x⁶/x⁸ = 81

x^{4 + 6} / x⁸ = 81

x¹⁰ / x⁸ = 81

x^{10 - 8} = 81

x² = 81

So, the value of x² is 81. Then option a is correct.

Example 13 :

If x⁶  = 60 and w¹⁰ =  20, what is x¹² w^-10 ?

a)  36     b)  60      c)  120    d)  180     e)  360

Solution :

x⁶  = 60 and w¹⁰ =  20

From x⁶  = 60, we raise power 2

(x⁶)² = (60)²

x¹² = (60)²

From w¹⁰ =  20, we raise power -1 we get

(w¹⁰)^-1 =  20^-1

w^-10 =  20^-1

w^-10 =  1/20

x¹² w^-10 = (60)²(1/20)

= 3600/20

= 180

So, option d is correct.

Example 14 :

If a² = b, what is a⁴ in terms of b ?

a)  2b     b)  b + 2      c)  2b + 2    d)  b²     e)  4b

Solution :

a² = b

Raising power 2 on both sides, we get

(a²)² = b²

a⁴ = b²

So, option d is correct.

Example 15 :

If x³ = y⁹, what is x in terms of y ?

a)  √y     b)  y²      c)  y³     d)  y⁶      e)  y¹² 

Solution :

x³ = y⁹

x = (y⁹)^1/3

= y^9/3

= y³

So, option c is correct.