EVALUATING COMPOSITION OF FUNCTIONS FROM TABLE

Use the table of values to evaluate each expression

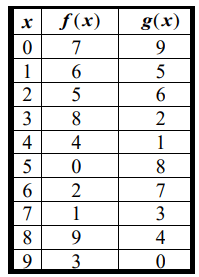
Problem 1 :

Find (f ∘ g) (8)

Solution :

(f ∘ g) (8) = f[g(8)]

When input = 8, the output g(8) is 4

= f[4]

When input = 4, the output f(4) is 4

(f ∘ g) (8) = 4

Problem 2 :

Find (f ∘ g) ( (5))

Solution :

(f ∘ g) (5) = f[g(5)]

When input = 5, the output g(5) is 8

= f[8]

When input = 8, the output f(8) is 9.

(f ∘ g) (5) = 9

Problem 3 :

Find (g ∘ f) (5)

Solution :

(g ∘ f) (5) = g[f(5)]

When input  = 5, the value of f(5) = 0

= g[0]

When input = 0, the value of g(0) = 9

= 9

Problem 4 :

Evaluate (g ∘ f) ( (3))

Solution :

(g ∘ f) (3)

When input  = 3, the value of f(3) = 8

= g[8]

When input = 0, the value of g(8) = 4

= 4

Problem 5 :

Evaluate (f ∘ f) (4)

Solution :

(f ∘ f) (4)

When input  = 4, the value of f(4) = 4

= f[4]

When input = 4, the value of f(4) = 4

= 4

Problem 6 :

Evaluate (f ∘ f) (1)

Solution :

(f ∘ f) (1)

When input  = 1, the value of f(1) = 6

= f[6]

When input = 6, the value of f(6) = 2

= 2

Problem 7 :

Evaluate (g ∘ g) (2)

Solution :

(g ∘ g) (2) = g[g(2)]

When input  = 2, the value of g(2) = 6

= g[6]

When input = 6, the value of g(6) = 7

= 7

Problem 8 :

Evaluate (g ∘ g) (6)

Solution :

(g ∘ g) (6) = g[g(6)]

When input = 6, the value of g(6) = 7

= g[7]

When input = 7, the value of g(7) = 3

= 3

Problem 9 :

Using the tables below, evaluate (f ∘ g)(3) and (g ∘ f) (4)

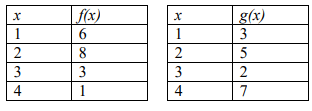
Solution :

i)  (f ∘ g)(3) = f[g(3)]

When x = 3, the output for g(3) will be 2.

= f(2)

When x = 2, the output for f(2) will be 8.

(f ∘ g)(3) = 8

ii)  (g ∘ f) (4) = g[f(4)]

When x = 4, the output for f(4) will be 1.

= g (1)

When x = 1, the output for g(1) will be 3.

(g ∘ f) (4) = 3

Problem 10 :

Given

f(2) = 3, f(3) = 4, f(5) = 0, g(2) = 5, g(3) = 2, and g(4) = -1,

evaluate the following. 

a) f(g(3))      b) f(g(2))    c) g(f(2))        d) g(f(3))

Solution :

From the given inputs and outputs, we can create a table.

a) f(g(3)) = f(2) ==> 3

b) f(g(2)) = f(5) ==> 0

c) g(f(2)) = g(3) ==> 2

d) g(f(3)) = g(4) ==> -1

Problem 11 :

Let

f = {(1, 5), (2, 6), (3, 7)} and g = {(5, 10), (6, 11), (7, 0)}.

Explain how each equation is true. 

a) g(f(1)) = 10             b) g(f(3)) = 0

Solution :

a) g(f(1)) = 10

In f(1), when input = 1, the output = 5

g(f(1)) = g(5)

= 10

So, a is true.

b) g(f(3)) = 0

In f(3), when input = 3, the output = 7

g(f(3)) = g(7)

= 0

So, b is true.

Problem 12 :

Use the arrow mappings to find the following

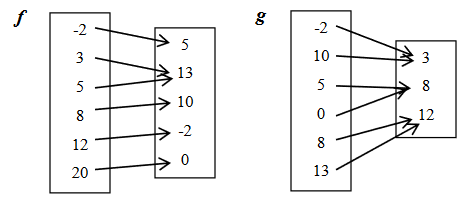
a) (f ∘ g) (10)

b)  (g ∘ f) (-2)

c)  (g ∘ f) (6)

d)  f[g(f(20)]

e)  f [ g(g(0)) ]

Solution :

a) (f ∘ g) (10) = f[g(10)] = f(3) ==> 13

b)  (g ∘ f) (-2) = g[f(-2)] = g(5) ==> 8

c)  (g ∘ f) (6) = g[f(6)] 

Since f(6) is undefined, (g ∘ f) (6) = undefined.

d)  f[g(f(20)]

The value of f(20) = 0

f[g(f(20)] = f[g(0)]

The value of g(0) = 8

f[g(0)] = f(8)

The value of f(8) is 10.

f[g(f(20)] = 10

e)  f [ g(g(0)) ]

The value of g (0) = 8

f[g(g(0)] = f[g(8)]

The value of g(8) = 10

f[g(8)] = f(10)

= undefined