EVALUATING COMPOSITION OF FUNCTIONS FROM TABLE
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Use the values in the table to evaluate the indicated composition of functions.
Example 1 :
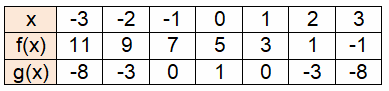
|
(i) (f ∘ g) (1) (ii) (g ∘ f) (2) (iii) (g ∘ g) (1) |
(iv) (f ∘ g) (2) (v) (g ∘ f) (3) (vi) (f ∘ f) (3) |
Solution :
(i) (f ∘ g) (1) = f [g(1)]
The value of g(1) from the table is 0. So replacing g(1) by 0.
f [g(1)] = f(0)
The value of f(0) from the table is 5.
f(0) = 5
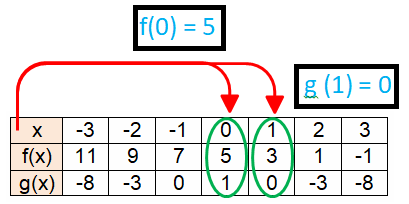
(ii) (g ∘ f) (2) = g [f(2)]
The value of f(2) from the table is 1. So replacing f(2) by 1.
g [f(2)] = g(1)
The value of g(1) from the table is 0.
g(1) = 0
(iii) (g ∘ g) (1) = g [g(1)]
The value of g(1) from the table is 0. So replacing g(1) by 0.
g [g(1)] = g(0)
The value of g(0) from the table is 1.
g(0) = 1
(iv) (f ∘ g) (2) = f [g(2)]
The value of g(2) from the table is -3. So replacing g(2) by -3.
f [g(2)] = f(-3)
The value of f(-3) from the table is 11.
f(-3) = 11
(v) (g ∘ f) (3) = g [f(3)]
The value of f(3) from the table is -1. So replacing f(3) by -1.
g [f(3)] = g(-1)
The value of g(-1) from the table is 0.
g(-1) = 0
(vi) (f ∘ f) (3) = f [f(3)]
The value of f(3) from the table is -1. So replacing f(3) by -1.
f [f(3)] = f(-1)
The value of f(-1) from the table is 7.
f(-1) = 7
Example 2 :
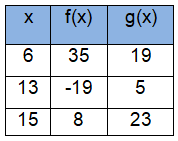
(i) f(13)
(ii) f(6)
(iii) g(15)
(iv) g(13)
(v) For what value of x, f(x) = 35 ?
(vi) For what value of x, g(x) = 5 ?
Solution :
(i) f(13) = -19
(ii) f(6) = 35
(iii) g(15) = 23
(iv) g(13) = 5
(v) f(x) = 35, when x = 6.
(vi) g(x) = 5, when x = 13.
Example 3 :
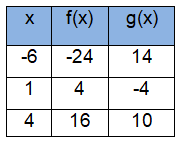
(i) f(4) =
(ii) g(1) =
(iii) g(4) =
(iv) g(-6) =
(v) For what value of x, f(x) is -24 ?
(vi) For what value of x, f(x) is 4 ?
Solution :
(i) f(4) = 16
(ii) g(1) = -4
(iii) g(4) = 10
(iv) g(-6) = 14
Example 4 :
A consumer advocacy company conducted a studyt to research the pricing of fruit and vegetables. They collected data on the size and price of prduce items, including navel oranges. They found that for the given chain of stores, the price of ornages was the function of the weight of the oranges p = f(w)

The company also determined that the weight of the oranges measured was the function of the radius of the oranges w = g(r)
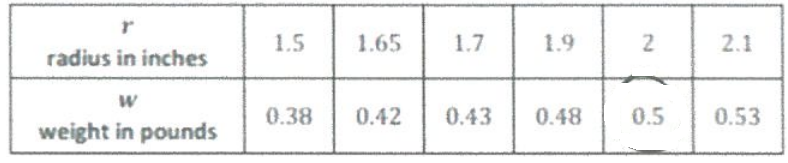
Use the table to evaluate f(g(2)).
Solution :
f(g(2)) = f[g(2)]
Finding the value of g(2), from the table we get g(3) = 0.5
= f(0.5)
Value of f(0.5) is 0.65
f(g(2)) = 0.65
A soda factory makes it is own carbonated water. The cost of a bottle of soda depends on the yield of carbon dioxide to water. The yield will vary with temperature. The cost to manufacture the soda is c = b(g).
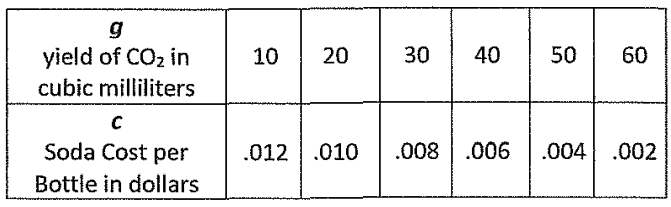
The yield of carbon dioxide is a function of temperature g = f(t).
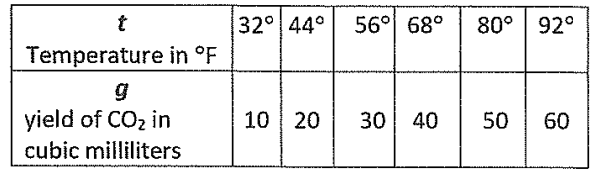
Use the tables to evaluate:
a) b(f(68°)) =
b) b(f(56°)) =
Solution :
a) b(f(68°)) = b[ f(68) ]
f(68°) = 40
b[ f(68) ] = b(40)
= 0.006
So, the value of b(f(68°)) is 0.006.
b) b(f(56°)) = b[ f(56°) ]
The value of f(56) is 30
f(56) = 30
b[ f(56°) ] = b[30]
b[ f(56°) ] = 0.008
Example 5 :
If 𝑓(𝑥) = 3𝑥 − 2 𝑎𝑛𝑑 𝑔(𝑥) = 3𝑥 + 𝑏, find 𝑏 such that (𝑓 ◦𝑔)(𝑥) = (𝑔 ◦ 𝑓)(𝑥) for all real numbers 𝑥.
Solution :
𝑓(𝑥) = 3𝑥 −2 𝑎𝑛𝑑 𝑔(𝑥) = 3𝑥+𝑏,
(𝑓 ◦𝑔)(𝑥) = f[g(x)]
= f[3x + b]
Applying x = 3x + b in the function f(x)
= 3(3x + b) - 2
= 9x + 3b - 2 ------(1)
)Using the given tables, find (f∘g) (2)
(g ◦ f)(𝑥) = g[f(x)]
= g[3x - 2]
Applying x = 3x - 2 in the function g(x).
= 3(3x - 2) + b
= 9x - 6 + b ------(2)
(1) = (2)
9x + 3b - 2 = 9x - 6 + b
9x - 9x + 3b - b = -6 + 2
2b = -4
b = -2
So, the require value of b is -2.
Example 6 :
Using the given tables, find (f ∘ g) (2)
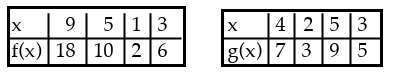
a) 6 b) 10 c) 3 d) 2
Solution :
(f ∘ g) (2) = f[g(2)]
Applying the value of g(2), we get
= f[3]
Applying the value of f(3), we get
= 6
So, option a is correct.
Example 7 :
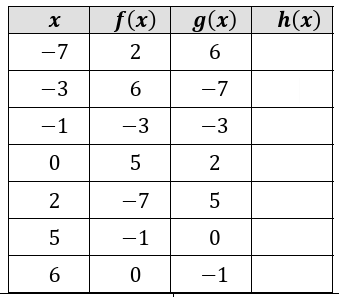
Fill in the following table, given that ℎ(𝑥) = 𝑓(𝑔(𝑥))
Solution :
ℎ(𝑥) = 𝑓(𝑔(𝑥))
|
ℎ(-7) = 𝑓(𝑔(-7)) = f(6) ℎ(-7) = 0 |
ℎ(-3) = 𝑓(𝑔(-3)) = f(-7) ℎ(-3) = 2 |
ℎ(-1) = 𝑓(𝑔(-1)) = f(-3) ℎ(-1) = 6 |
ℎ(0) = 𝑓(𝑔(0)) = f(2) ℎ(0) = -7 |
|
ℎ(2) = 𝑓(𝑔(2)) = f(5) ℎ(2) = -1 |
ℎ(5) = 𝑓(𝑔(5)) = f(0) ℎ(5) = 5 |
ℎ(6) = 𝑓(𝑔(6)) = f(-1) ℎ(6) = -3 |
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling