EVALUATING COMPOSITOION OF FUNCTION FROM TABLE
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
If f and g are functions, then the composite function of f and g is defined by
(f ∘ g)(x) = f( g(x) )
The domain of (f ∘ g) is the set of all real numbers x in the domain of g such that ݃g(x) is in the domain of f.
Problem 1 :
Use the table of values to evaluate each expression
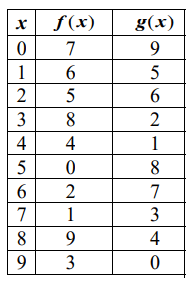
|
1) f ( g(8) ) 4) g ( f (3) ) 7) g ( g (2) ) |
2) f( g(5) ) 5) f ( f (4) ) 8) g ( g (6) ) |
3) g ( f (5) ) 6) f ( f (1) ) 9) g ( g (1) ) |
Solution :
1) f ( g(8) )
From the table, value of g(8) is 4.
f ( g(8) ) = f(4)
= 4
2) f ( g(5) )
From the table, value of g(5) is 8.
f ( g(5) ) = f(8)
= 9
3) g ( f (5) )
From the table, value of f(5) is 0.
g ( f(5) ) = f(0)
= 7
4) g ( f (3) )
From the table, value of f(3) is 8.
g ( f(3) ) = f(8)
= 9
5) f ( f (4) )
From the table, value of f(4) is 4.
f ( f(4) ) = f(4)
= 4
6) f ( f (1) )
From the table, value of f(1) is 6.
f ( f(1) ) = f(6)
= 2
7) g ( g (2) )
From the table, value of g(2) is 6.
f ( f(1) ) = f(6)
= 2
8) g ( g (6) )
From the table, value of g(6) is 7.
g ( g(6) ) = g(7)
= 1
9) g ( g (1) )
From the table, value of g(1) is 5.
g ( g(1) ) = g(5)
= 8
Problem 2 :
Evaluating Composite Functions :
The tables give some selected ordered pairs for functions f and g
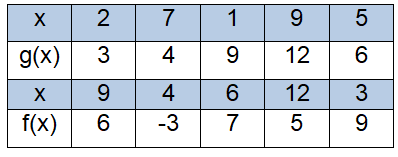
|
1) (f ∘ g)(2) 2) (f ∘ g)(1) 3) (f ∘ g)(9) |
4) (f ∘ g)(5) 5) (g ∘ f)(6) 6) (f ∘ g)(7) |
7) (g ∘ f)(12) 8) (g ∘ f)(3) |
Solution :
1) (f ∘ g)(2)
(f ∘ g)(2) = f [ g(2) ] ----(1)
The value of g(2) is 3.
Applying it in (1), we get
= f [ 3 ]
(f ∘ g)(2) = 9
2) (f ∘ g)(1)
(f ∘ g)(1) = f [ g(1) ] ----(1)
The value of g(1) is 9.
Applying it in (1), we get
= f [ 9 ]
(f ∘ g)(9) = 6
3) (f ∘ g)(9)
(f ∘ g)(9) = f [ g(9) ] ----(1)
The value of g(9) is 12.
Applying it in (1), we get
= f [ 12 ]
(f ∘ g)(12) = 5
4) (f ∘ g)(5)
(f ∘ g)(5) = f [ g(5) ] ----(1)
The value of g(5) is 6.
Applying it in (1), we get
= f [ 6 ]
(f ∘ g)(6) = 7
5) (g ∘ f)(6)
(g ∘ f)(6) = g [ f(6) ] ----(1)
The value of f(6) is 7.
Applying it in (1), we get
= f [ 7 ]
(g ∘ f)(6) = -3
6) (f ∘ g)(7)
(f ∘ g)(7) = f [ g(7) ] ----(1)
The value of g(7) is 4.
Applying it in (1), we get
= f [ 4 ]
(f ∘ g)(7) = -3
7) (g ∘ f)(12)
(g ∘ f)(12) = g [ f(12) ] ----(1)
The value of f(12) is 5.
Applying it in (1), we get
= g [ 5 ]
(g ∘ f)(12) = 6
8) (g ∘ f)(3)
(g ∘ f)(3) = g [ f(3) ] ----(1)
The value of f(3) is 9.
Applying it in (1), we get
= g [ 9 ]
(g ∘ f)(3) = 12
Problem 3 :
Use the tables of ordered pairs to determine the value of each composite function

|
1) (𝑓 ∘ 𝑔)(36) = 2) (𝑔 ∘ 𝑔)(16) = |
3) (𝑔 ∘ 𝑓)(4) = 4) (𝑓 ∘ 𝑓)(4) = |
Solution :
|
1) (𝑓 ∘ 𝑔)(36) = 𝑓 [ 𝑔(36) ] = f[6] = 21 |
2) (𝑔 ∘ 𝑔)(16) = = g [ 𝑔(16) ] = g[4] = 2 |
|
3) (𝑔 ∘ 𝑓)(4) = = g [ f(4) ] = g[1] = 1 |
4) (𝑓 ∘ 𝑓)(4) = = f [ f(4) ] = f[1] = -14 |
Problem 4 :
The table below shows values of 𝑓(𝑥) at selected values of 𝑥. The function 𝑔(𝑥) is shown in the graph below.
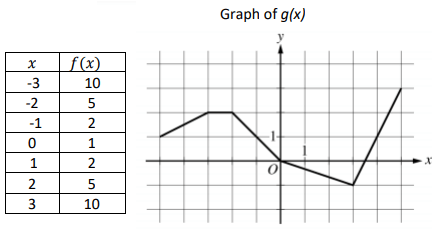
Let h be the function defined by ℎ(𝑥) = 2|𝑥 − 4|.
Find:
|
1. 𝑦 = ℎ(𝑓(2)) 2. 𝑦 = ℎ(𝑔(3)) 3. 𝑦 = 𝑔(𝑓(−2)) |
4. 𝑦 = 𝑓(𝑔(−3)) 5. 𝑦 = 𝑔(𝑓(ℎ(3))) 6. Find ℎ(𝑓(𝑔(0))) |
Solution :
1. 𝑦 = ℎ(𝑓(2))
From the table value of f(2) is 5.
y = h(5)
Given ℎ(𝑥) = 2|𝑥 − 4|
h(5) = 2|5 - 4|
y = h(5) = 2
2. 𝑦 = ℎ(𝑔(3))
From the graph, the value of g(3) is -1.
y = h(-1)
Given ℎ(𝑥) = 2|𝑥 − 4|
h(-1) = 2|-1 - 4|
y = h(-1) = 10
3. 𝑦 = 𝑔(𝑓(−2))
y = g(5)
From the table, value of f(-2) is 5.
y = g(5)
y = 3
4. 𝑦 = 𝑓(𝑔(−3))
From the graph, value of g(-3) is 2.
𝑦 = 𝑓(2)
From the table, the value of f(2) is 5.
y = 5
5. 𝑦 = 𝑔(𝑓(ℎ(3)))
From the given function, value of h(3) is
ℎ(3) = 2|3 − 4|
h(3) = 2
𝑦 = 𝑔(𝑓(2))
Value of f(2) is 5.
𝑦 = 𝑔(5)
From the table, the value of g(5) is 3.
y = 3
6. Find ℎ(𝑓(𝑔(0)))
From the graph, the value of g(0) = 0
y = ℎ(𝑓(0))
From the table, the value of f(0) is 1.
𝑦 = h(1)
ℎ(1) = 2|1 − 4|
h(2) = 6
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling