EVALUATING COMPOSITE INVERSE TRIG FUNCTIONS

To evaluate composite inverse trig functions, we should aware of reference triangle.

A reference triangle is formed by "dropping" a perpendicular from the terminal ray of a standard position angle to the x-axis. Remember, it must be drawn to the x-axis

With the help of formulas given above, we will rewrite the given inverse trig functions in terms of other inverse trig functions.

Find the exact value of each expression.

Problem 1 :

cos sin-1 45

Solution :

Given, cos sin-1 45sin 𝜃 = oppositehypotenusecos 𝜃 = adjacenthypotenuse

Using reference triangle.

eva-com-in-trig-fun-s1

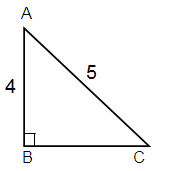
Here, Opposite = 4, Hypotenuse = 5

AC2 = AB2 + BC2

52 = 42 + BC2

25 = 16 + BC2

25 - 16 = BC2

9 = BC2

BC = √9

BC = 3

cos sin-1 45 = 35

Problem 2 :

sin tan-1 724

Solution :

Given, sin tan-1 724tan 𝜃 = oppositeadjacentsin 𝜃 = oppositehypotenuse

Using reference triangle.

eva-com-in-trig-fun-s2

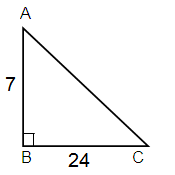
 Here Opposite = 7, Adjacent = 24

AC2 = AB2 + BC2

= 72 + 242

= 49 + 576

AC2 = 625

AC = √625

AC = 25

sin tan-1 724 = 725

Problem 3 :

tan cos-1 513

Solution :

Given, tan cos-1 513cos 𝜃 = adjacenthypotenusetan 𝜃 = oppositeadjacent

Using reference triangle.

eva-com-in-trig-fun-s3

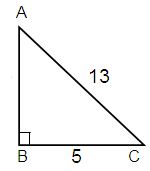
Here Adjacent = 5, Hypotenuse = 13

AC2 = AB2 + BC2

132 = AB2 + 52

169 = AB2 + 25

169 - 25 = AB2

144 = AB2

AB = √144

AB = 12

tan cos-1 513 = 125

Problem 4 :

cot sin-1 513

Solution :

Given,cot sin-1 513sin 𝜃 = oppositehypotenusecot 𝜃 = adjacentopposite

Using reference triangle.

eva-com-in-trig-fun-s4

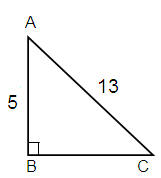
 Here Opposite = 5, Hypotenuse = 13

AC2 = AB2 + BC2

132 = 52 + BC2

169 = 25 + BC2

169 - 25 = BC2

BC2  = 144

BC = √144

BC = 12

cot sin-1 513 = 125

Problem 5 :

tan sin-1 -35

Solution :

Given,tan sin-1 -35 sin 𝜃 = oppositehypotenusetan 𝜃 = oppositeadjacent

Using reference triangle.

eva-com-in-trig-fun-s5

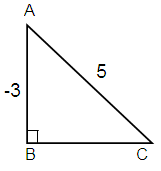
Here Opposite = = -3, Hypotenuse = 5

AC2 = AB2 + BC2

52 = (-3)2 + BC2

25 = 9 + BC2

BC2 = 25 - 9

BC2 = 16

BC = √16

BC = 4

tan sin-1 -35 = -34

Problem 6 :

cos sin-1 -45

Solution :

Given, cos sin-1 -45sin 𝜃 = oppositehypotenusecos 𝜃 = adjacenthypotenuse

Using reference triangle.

eva-com-in-trig-fun-s6

Here Opposite = = -4, Hypotenuse = 5

AC2 = AB2 + BC2

52 = (-4)2 + BC2

25 = 16 + BC2

BC2 = 16 - 25

BC2 = -9

BC =  √-9

BC = 3

cos sin-1 -45 = 35

Problem 7 :

cot tan-1 73

Solution :

Given, cot tan-1 73tan 𝜃 = oppositeadjacentcot 𝜃 = adjacentopposite

Using reference triangle.

eva-com-in-trig-fun-s7

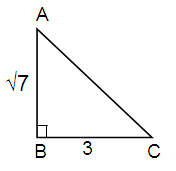
 Here Opposite = √7, Adjacent = 3

= 1tan tan-1 73= 173= 37= 37 × 77= 377cot tan-1 73 = 377

Problem 8 :

sin tan-1 22

Solution :

Given,sin tan-1 22 tan 𝜃 = oppositeadjacentsin 𝜃 = oppositehypotenuse

Using reference triangle.

eva-com-in-trig-fun-s8

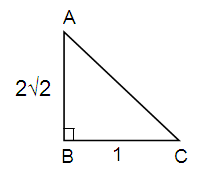
 Here Opposite = 2√2, Adjacent = 1

AC2 = AB2 + BC2

= (2√2)2 + 12

= 8 + 1

= 9

AC2 = 9

AC = √9

AC = 3

sin tan-1 22 = 223

Problem 9 :

cot sec-1 76

Solution :

Given, cot sec-1 76sec 𝜃 = hypotenuseadjacentcot 𝜃 = adjacentopposite

Using reference triangle.

eva-com-in-trig-fun-s9

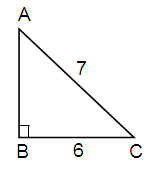
Here Hypotenuse = 7, Adjacent = 6

AC2 = AB2 + BC2

72 = AB2 + 62

49 = AB2 + 36

49 - 36 = AB2

13 = AB2

AB = √13

cot sec-1 76 = 613Numerator and denominator multiplying by 13.= 613 × 1313= 61313cot sec-1 76 = 61313

Problem 10 :

sin cos-1 217

Solution :

Given, sin cos-1 217 cos 𝜃 = adjacenthypotenusesin 𝜃 = oppositehypotenuse

Using reference triangle.

eva-com-in-trig-fun-s10

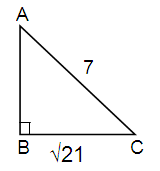
Here Adjacent = √21, Hypotenuse = 7

AC2 = AB2 + BC2

72 = AB2 +  (√21)2

49 = AB2 + 21

49 - 21 = AB2

28 = AB2

AB =  √28

AB = 2√7

sin cos-1 217 = 277

Problem 11 :

sin arctan -113

Solution :

Given, sin arctan -113 tan 𝜃 = oppositeadjacentsin 𝜃 = oppositehypotenuse

Using reference triangle.

eva-com-in-trig-fun-s11

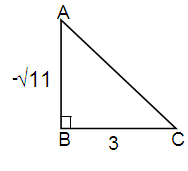
 Here Opposite = -√11, Adjacent = 3

AC2 = AB2 + BC2

= (-√11)2 + 32

= 11 + 9

= 20

AC = √20

AC = 2√5

sin arctan -113 = -1125Numerator and denominator multiplying by 5.= -1125 × 55= -552 × 5sin arctan -113= -5510

Problem 12 :

sin arcsec 72

Solution :

Given, sin arcsec 72sec 𝜃 = hypotenuseadjacentsin 𝜃 = oppositehypotenuse
eva-com-in-trig-fun-s12

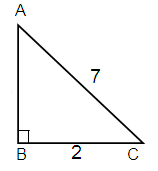
Here  Hypotenuse = 7,  Adjacent = 2

AC2 = AB2 + BC2

72 = AB2 +  22

49 = AB2 + 4

49 - 4 = AB2

45 = AB2

AB = √45

AB = 3√5 

sin arcsec 72 = 357

Recent Articles

RSS

  1. Finding Range of Values Inequality Problems

    May 21, 24 08:51 PM

    Finding Range of Values Inequality Problems

    Read More

  2. Solving Two Step Inequality Word Problems

    May 21, 24 08:51 AM

    Solving Two Step Inequality Word Problems

    Read More

  3. Exponential Function Context and Data Modeling

    May 20, 24 10:45 PM

    Exponential Function Context and Data Modeling

    Read More