EVALUATING COMPOSITE FUNCTIONS FROM GRAPHS

Problem 1 :

Find f(-3) + g(-3).

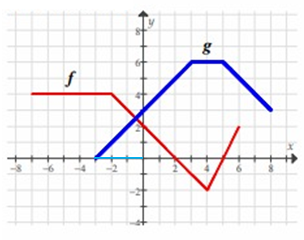
Solution :

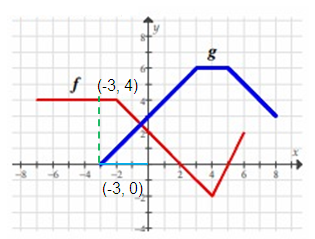
f(-3) + g(-3) = 4 + 0

= 4 

Problem 2 :

Find f(0) + g(0).

Solution :

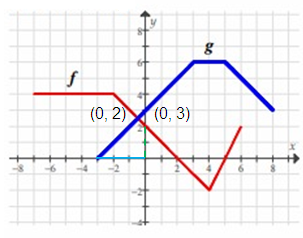
f(0) + g(0) = 2 + 3

= 5 

Problem 3 :

Find f(-6) + g(-6).

Solution :

By observing the graph, f(-6) is 4, for g(-6) we dont see the part of the graph. So, for g(-6) it is undefined.

Problem 4 :

Find f(5) + g(5).

Solution :

f(5) + g(5) = 0 + 6

= 6

Problem 5 :

Find f(7) + g(7).

Solution :

Observing the graph, f(7) = undefined

g(7) = 4

f(7) + g(7) = undefined + 4

= undefined

Problem 6 :

Sketch the graph of f + g. (Hint : For any x value, add the y values of f and g.) 

Solution :

By connecting the following points, we will get the graph of the composition function.

(-3, 4)(-2, 5)(-1, 5)(0, 5)(1, 5)(2, 5)(3, 5)(4, 4)(5, 6)(6, 7)

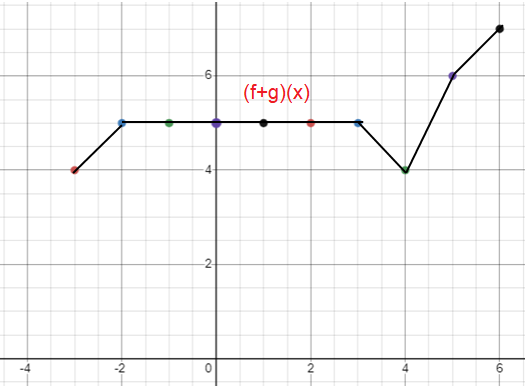
Problem 7 :

What is the domain of f + g ? Explain how you obtained your answer.

Solution :

Domain : The set of all x - coordinates.

We can see both graphs f(x) and g(x) in between the interval

[-3, 6]

So, domain is [-3, 6].

Use the graph to answer for the questions given below.

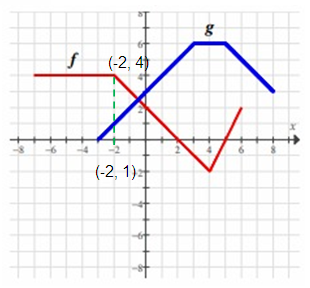
Problem 8 :

Find f(-2) - g(-2).

Solution :

f(-2) - g(-2) = 4 - 1

= 3

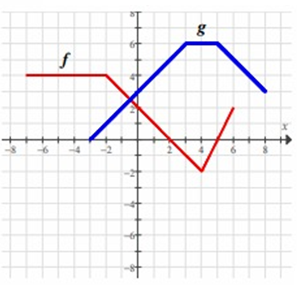
Problem 9 :

Find f(0) - g(0).

Solution :

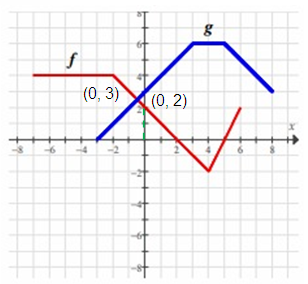
f(0) - g(0) = 2 - 3

= -1

Problem 10 :

Find f(-4) - g(-4).

Solution :

We see the graph f(-4) is 4, but g(-4) is undefined. So,

f(-4) - g(-4) = undefined.

Problem 11 :

f(2) - g(2)

Solution :

f(2) - g(2) = 0 - 5

= -5

Problem 12 :

f(4) - g(4)

Solution :

f(4) - g(4) = -2 - 6

= -8

Problem 13 :

Sketch the graph of f - g. (Hint : For any x value, subtract the y values of f and g.) 

Solution :

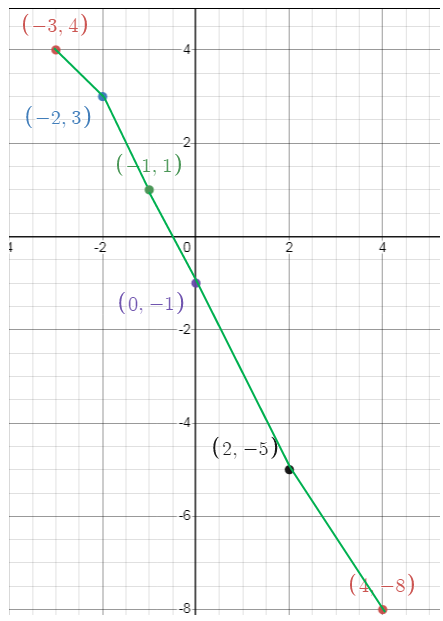
Problem 14 :

What is the domain of f - g ? Explain how you obtained your answer.

Solution :

By observing the graph above, we get domain as

[-3, 8]