EVALUATE TRIGONOMETRIC FUNCTIONS GIVEN A POINT

Use the given point on the terminal side of angle θ to find the value of the trigonometric function indicated.

Problem 1 :

csc θ 

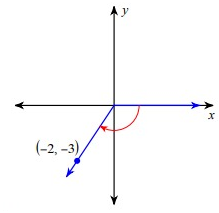
Solution :

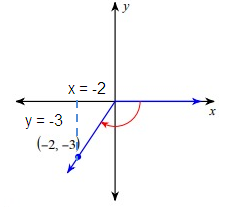
Since the terminal side lies in the third quadrant, for the trigonometric ratios tan θ and cot θ, we will have positive.

cosec θ = hypotenuse/opposite

Let 'r' be the hypotenuse.

By using Pythagorean theorem.

r² = x² + y²

= (-2)² + (-3)²

= 4 + 9

r² = 13

r = √13

cosec θ = √13/-3

cosec θ = -√13/3

Problem 2 :

csc θ 

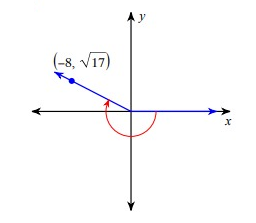
Solution :

Since the terminal side lies in the second quadrant, for the trigonometric ratios sin θ and cosec θ, we will have positive.

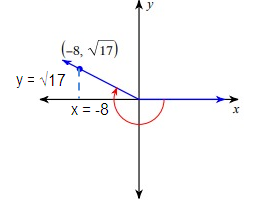
cosec θ = hypotenuse/opposite

Let 'r' be the hypotenuse.

By using Pythagorean theorem.

r² = x² + y²

= (-8)² + (√17)²

= 64 + 17

r² = 81

r = 9

csc θ = 9/√17

Problem 3 :

cos θ 

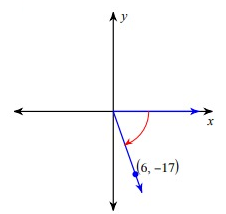
Solution :

Since the terminal side lies in the fourth quadrant, for the trigonometric ratios cos θ and sec θ, we will have positive.

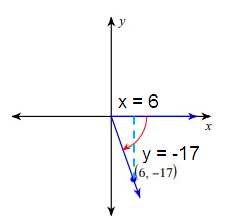
cos θ = adjacent/hypotenuse

Let 'r' be the hypotenuse.

By using Pythagorean theorem.

r² = x² + y²

= (6)² + (-17)²

= 36 + 289

r² = 325

r = 5√15

cos θ = 6/5√15

Problem 4 :

csc θ 

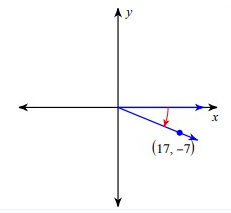
Solution :

Since the terminal side lies in the fourth quadrant, for the trigonometric ratios cos θ and sec θ, we will have positive.

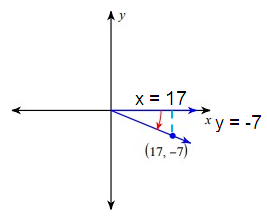
cosec θ = hypotenuse/opposite

Let 'r' be the hypotenuse.

By using Pythagorean theorem.

r² = x² + y²

= (17)² + (-7)²

= 289 + 49

r² = 338

r = 13√2

cosec θ = 13√2/-7

cosec θ = -13√2/7

Problem 5 :

cot θ

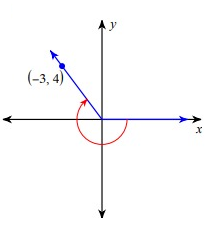
Solution :

Since the terminal side lies in the second quadrant, for the trigonometric ratios sin θ and cosec θ, we will have positive.

cot θ = adjacent/opposite

= -3/4

cot θ = -3/4

Problem 6 :

cot θ

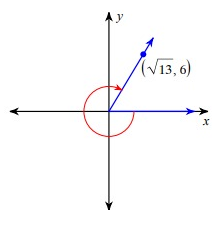
Solution :

Since the terminal side lies in the first quadrant, for all trigonometric ratios it is positive.

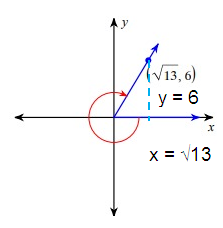
cot θ = adjacent/opposite

= √13/6

Problem 7 :

cos θ

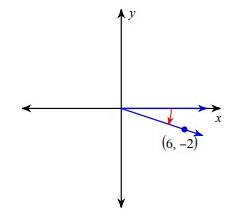
Solution :

Since the terminal side lies in the fourth quadrant, for the trigonometric ratios cosθ and secθ it is positive.

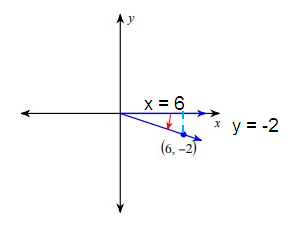
cos θ = adjacent/hypotenuse

Let 'r' be the hypotenuse.

By using Pythagorean theorem.

r² = x² + y²

= (6)² + (-2)²

= 36 + 4

r² = 40

r = √40

cos θ = 6/√40

Problem 8 :

cos θ

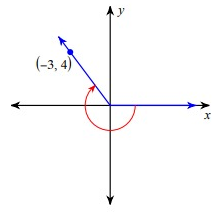
Solution :

Since the terminal side lies in the second quadrant, for the trigonometric ratios sin θ and cosecθ it is positive.

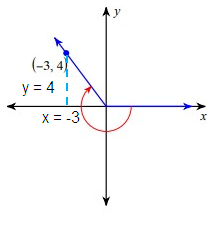
cos θ = adjacent/hypotenuse

Let 'r' be the hypotenuse.

By using Pythagorean theorem.

r² = x² + y²

= (-3)² + (4)²

= 9 + 16

r² = 25

r = 5

cos θ = -3/5

Problem 9 :

csc θ

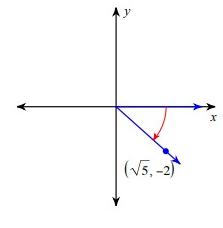
Solution :

Since the terminal side lies in the fourth quadrant, for the trigonometric ratios cos θ and secθ it is positive.

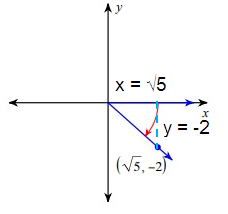
cosec θ = hypotenuse/opposite

Let 'r' be the hypotenuse.

By using Pythagorean theorem.

r² = x² + y²

= (√5)² + (-2)²

= 5 + 4

r² = 9

r = 3

cosec θ = 3/-2

cosec θ = -3/2

Problem 10 :

csc θ

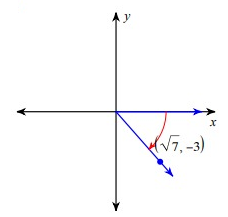
Solution :

Since the terminal side lies in the fourth quadrant, for the trigonometric ratios cos θ and secθ it is positive.

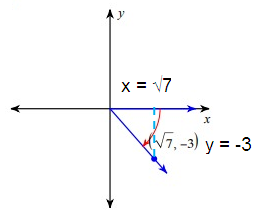
cosec θ = hypotenuse/opposite

Let 'r' be the hypotenuse.

By using Pythagorean theorem.

r² = x² + y²

= (√7)² + (-3)²

= 7 + 9

r² = 16

r = 4

cosec θ = 4/-3

cosec θ = -4/3