EVALUATE THE LIMITS FROM THE GIVEN GRAPH

Evaluating Left hand and right hand limit

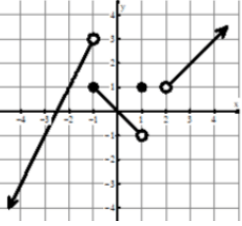
Problem :

Evaluate the following :

1) lim _x->-1^-   f(x)

2) lim _x->-1⁺   f(x)

Solution :

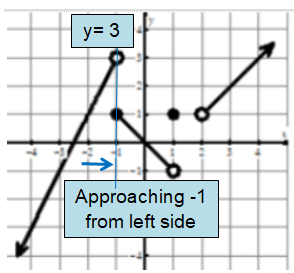
1) lim _x->-1^-   f(x) = 3

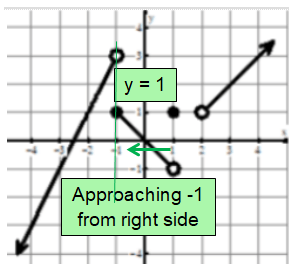
2) lim _x->-1⁺   f(x) = 1

When the limit does not exist ?

There are three situations

1) Jump discontinuity

2) there is a vertical asymptote

3) there is a violent oscillation

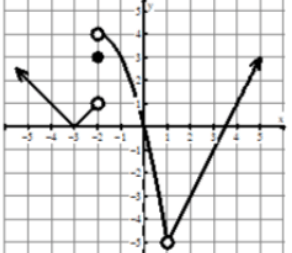
Problem :

Evaluate the following :

1) lim _x->-2^-   f(x)

2) lim _x->-2⁺   f(x)

3) lim _x->-2  f(x)

Solution :

1) lim _x->-2^-   f(x)

Approaching -2 from left side, we get the value of y as 1. So,

lim _x->-2^-  f(x) = 1

2) lim _x->-2⁺  f(x) = 4

Approaching -2 from right side, we get the value of y as 4. So,

lim _x->-2⁺  f(x) = 4

3) lim _x->-2  f(x)

Both left hand and right hand limits are not equal, the limit does not exists at x = -2.

lim _x->-2  f(x) = DNE

Limit does not exists when vertical there is vertical asymptote :

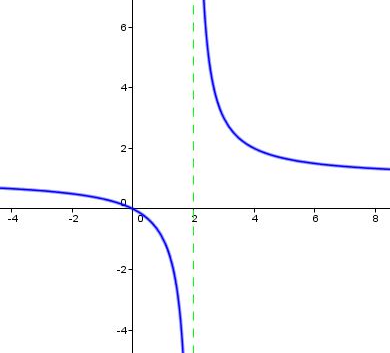
lim _x->2^-  f(x) = -inifnity

lim _x->2⁺  f(x) = inifnity

lim _x->2 f(x) = does not exists

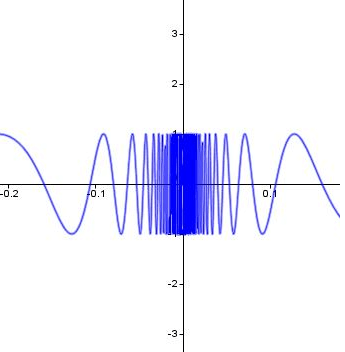
When the limit become undefined ?

lim _x->4^-  f(x) = 0

lim _x->4⁺  f(x) = inifnity

lim _x->4 f(x) = it is not a defined value, so undefined.

Problem 1 :

Use the graph of the function f(x) to answer each question. Use ∞, −∞ or DNE where appropriate.

Solution :

(a) f(0) :

The curve does not pass through any points on the y-axis. So, the answer is does not exists.

(b) f(2) :

The curve is passing through (2, 0). So, the value of f(2) is 0.

(c) f(3) :

We see the filled circle at (3, 3). So, the value of f(3) is 3.

(d) lim _x→0⁻ f(x) :

While approaching the value 0 from left side, the output becomes −∞. So, lim x→0⁻ f(x) = −∞.

(e) lim_x→0 f(x) :

At exactly x approaches 0, the output is 2.

lim_x→0 f(x) = 2.

(f) lim _x→3⁺ f(x) :

Approaching 3 from right side, the output is 2. So, lim _x→3⁺ f(x) = 2

(g) lim_x→3 f(x) :

Approaching 3 from left side, we get 1. Approaching 3 from right side, we get 2. On both sides, we get different value. So, lim_x→3 f(x) does not exists.

(h) lim x→−∞ f(x)

At y = 1, we see the horizontal asymptote, x approaches infinity. So, the required output at x→−∞ is 1.

lim x→−∞ f(x) = 1

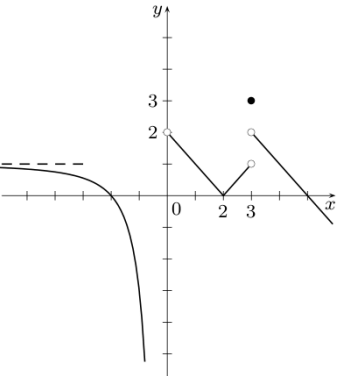
Problem 2 :

Use the graph of the function f(x) to answer each question. Use ∞, −∞ or DNE where appropriate.

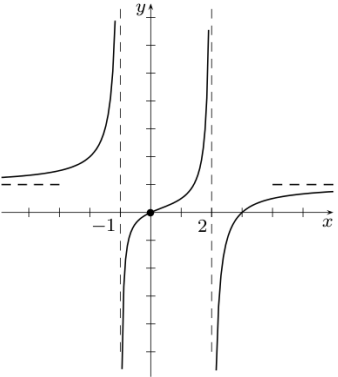
Solution :

By observing the graph above, at y = 1, we see horizontal asymptote. We see vertical asymptotes at x = -1 and x = 2,

(a) f(0) :

When the input is 0, the output also is 0. So, f(0) = 0

(b) f(2) :

At x = 2, we have vertical asymptote, we dont know where the curve is going to intersect. Then value of f(2) does not exists.

(c) f(3) :

The curve is passing through the point (3, 0). So, the value of f(3) is 0.

(d) lim_x→−1 f(x) :

Approaching x = -1 on either sides, from left side it approaches + infinity, from the right side it approaches - infinity. Since they are not equal, lim_x→−1 f(x) does not exists.

(e) limx→0 f(x) :

Approaching 0 from either sides, we see that it gives 0. So, the value of lim_x→0 f(x) = 0

(f) lim _x→2+ f(x) :

Approaching 2 from right side, it approaches - infinity.

(g) lim_x→∞ f(x) :

When x approaches infinity, the output is 1. So, lim_x→∞ f(x) = 1

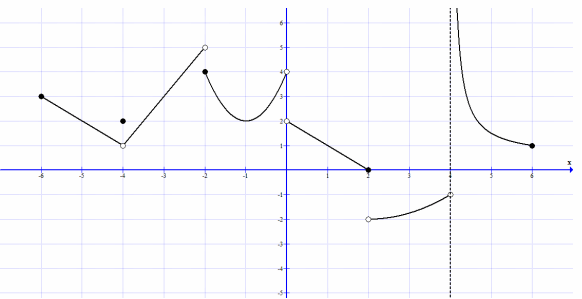
Problem 3 :

The graph of a function f is drawn above, answer the questions:

Solution :