EVALUATE THE FOLLOWING EXPRESSION USING PEMDAS

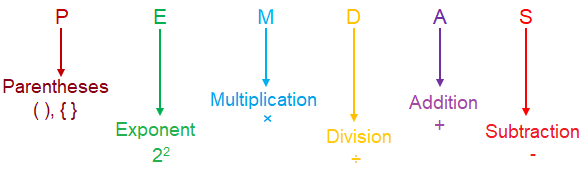
To evaluate the numerical expression, we need to know the order of operations.

What is an Order of Operations?

An Order of Operations is a rule that can be used to simplify or evaluate more than one operation.

There are many types of rules, we will use here the PEMDAS Rule.

Example 1 :

(20 + 80 ÷ 2 × 8) ÷ [(54 ÷ 9 + 14) ÷ 4]

Solution :

= (20 + 80 ÷ 2 × 8) ÷ [(54 ÷ 9 + 14) ÷ 4]

= (20 + 40 × 8) ÷ [(6 + 14) ÷ 4]

= (20 + 320) ÷ [20 ÷ 4]

= (20 + 320) ÷ 5

= 340 ÷ 5

= 68

P( ), D

P( ), M & A

P( ), [ ], A & D

P( ), A

D

Example 2 :

3 × [64 ÷ (13 - 5) - 4] × 42 ÷ 6

Solution :

= 3 × [64 ÷ (13 - 5) - 4] × 42 ÷ 6

= 3 × [64 ÷ 8 - 4] × 42 ÷ 6

= 3 × [8 - 4] × 42 ÷ 6

= 3 × 4 × 42 ÷ 6

= 12 × 42 ÷ 6

= 504 ÷ 6

= 84

P( ), S

P[ ], D

P[ ], S

M

M

D

Example 3 :

{24 ÷ [(8 × 3) ÷ 4] × 2} × (15 - 4)

Solution :

= {24 ÷ [(8 × 3) ÷ 4] × 2} × (15 - 4)

= {24 ÷ [24 ÷ 4] × 2} × 11

= {24 ÷ 6 × 2} × 11

= {4 × 2} × 11

= 8 × 11

= 88

P( ), M & S

P[ ], D

P{ }, D

P{ }, M

M

Example 4 :

[5 × (54 ÷ 6 - 3)] + 6 × 2 - 60

Solution :

= [5 × (54 ÷ 6 - 3)] + 6 × 2 - 60

= [5 × (9 - 3)] + 6 × 2 - 60

= [5 × 6] + 6 × 2 - 60

= 30 + 6 × 2 - 60

= 30 + 12 - 60

= 42 - 60

= -18

P( ), D

P( ), S

P[ ], M

M

A

S


Example 5 :

(78 - 6) ÷ {18 × [(7 - 8) × 2]}

Solution :

= (78 - 6) ÷ {18 × [(7 - 8) × 2]}

= 72 ÷ {18 × [-1 × 2]}

= 72 ÷ {18 × (-2)}

= 72 ÷ (-36)

= - 2

P( ), S

P[ ], M

P{ }, M

D

Example 6 :

{96 ÷ [36 ÷ 3 - (18 × 2 - 30)]} ÷ (31 - 16 + 1)

Solution :

= {96 ÷ [36 ÷ 3 - (18 × 2 - 30)]} ÷ (31 - 16 + 1)

= {96 ÷ [36 ÷ 3 - (36 - 30)]} ÷ (15 + 1)

= {96 ÷ [36 ÷ 3 - 6]} ÷ 16

= {96 ÷ [12 - 6]} ÷ 16

= {96 ÷ 6} ÷ 16

= 16 ÷ 16

= 1

P(), M&S

P(), S&A

P[ ], D

P[ ], S

P{ }, D

D

Example 7 :

2 × {11 + [2 × (10 - 15 + 8 × 3)] + 1}

Solution :

= 2 × {11 + [2 × (10 - 15 + 8 × 3)] + 1}

= 2 × {11 + [2 × (-5 + 24)] + 1}

= 2 × {11 + [2 × 19] + 1}

= 2 × {11 + 38 + 1}

= 2 × 50

= 100

P( ), M&S

P( ), S

P[ ], M

P{ }, A

M

Example 8 :

45 ÷ 15 × [(21 - 18) × (5 + 4 × 2) - 49]

Solution :

= 45 ÷ 15 × [(21 - 18) × (5 + 4 × 2) - 49]

= 45 ÷ 15 × [3 × (5 + 8) - 49]

= 45 ÷ 15 × [3 × 13 - 49]

=  45 ÷ 15 × [39 - 49]

= 45 ÷ 15 × (-10)

= 3 × (-10)

= -30

P( ), S&M

P( ), A

P[ ], M

P[ ], S

D

M

Example 9 :

9 ÷ 3 × {2 × [(16 × 4) ÷ 8]}

Solution :

= 9 ÷ 3 × {2 × [(16 × 4) ÷ 8]}

= 9 ÷ 3 × {2 × [64 ÷ 8]}

= 9 ÷ 3 × {2 × 8}

= 3 × 16

= 48

P( ), M

P[ ], D

P{ }, M

M

Example 10 :

100 - {4 × [3 × (19 + 1) ÷ 4]}

Solution :

= 100 - {4 × [3 × (19 + 1) ÷ 4]}

= 100 - {4 × [3 × 20 ÷ 4]}

= 100 - {4 × [3 × 5]}

= 100 - {4 × 15}

= 100 - 60

= 40

P( ), A

P[ ], D

P[ ], M

P{ }, M

S

Example 11 :

Peter has $450. He spends $210 on food. Later he divides all the money into four parts. The three parts were distaributed and one part he keeps for himself. Then, he found 50 cents on the road. Write the final expression and state the steps in finding the money left withe Peter.

Solution :

Writing expression, 

= (450 - 210) ÷ 4 + 0.50

= 240 ÷ 4 + 0.50

= 60 + 0.50

= 60.50

Example 12 :

Write the corresponding expression of the given problem below then simplify.

Flora bought 3 notebooks for $10 each, a box of pencils for $21 and a box of pens for $35. How much did he spend in all ?

Solution :

Number of notebooks = 3

Cost of each notebook = $10

Cost of box of pencils = $21

Cost of box of pens = $35

Required expression,

= 3(10) + 21 + 35

= 30 + 21 + 35

= $86

Recent Articles

RSS

  1. Finding Range of Values Inequality Problems

    May 21, 24 08:51 PM

    Finding Range of Values Inequality Problems

    Read More

  2. Solving Two Step Inequality Word Problems

    May 21, 24 08:51 AM

    Solving Two Step Inequality Word Problems

    Read More

  3. Exponential Function Context and Data Modeling

    May 20, 24 10:45 PM

    Exponential Function Context and Data Modeling

    Read More