EVALUATE THE COMPOSITION OF FUNCTIONS GRAPHICALLY 

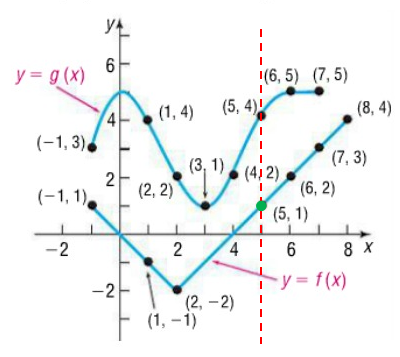
Use the graphs of f and g to evaluate each composite function.

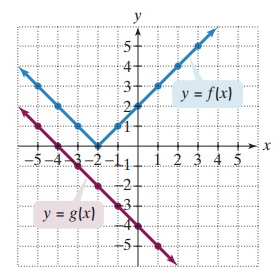
Problem 1 :

(f ∘ g)(-1)

Solution :

From the graphs given above, it is clear that the line is crossing the curve g(x) at -3.

The value of g(-1) is -3.

f(g(-1)) = f(-3)

When x = -3, the vertical line crosses the curve f(-3) at 1.

f(g(-1)) = 1

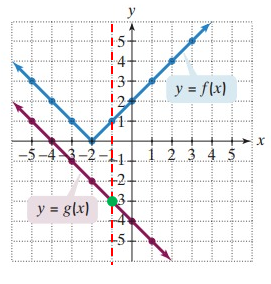
Problem 2 :

(f ∘ g)(1)

Solution:

From the graphs given above, it is clear that the line is crossing the curve g(x) at -5.

The value of g(1) is -5.

f(g(1)) = f(-5)

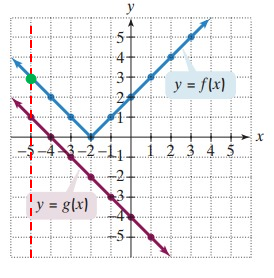
When x = -5, the vertical line crosses the curve f(-5) at 3.

f(g(1)) = 3

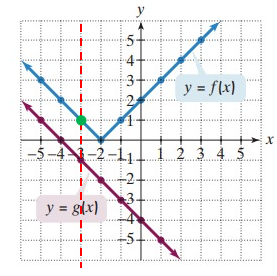
Problem 3 :

(g ∘ f)(0)

Solution:

(g ∘ f)(0) = g[f(0)]

= g(2)

g[f(0)]= -6

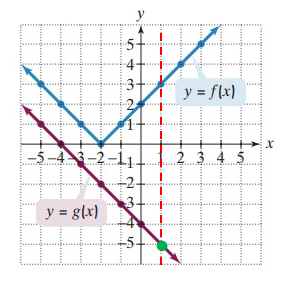
Problem 4 :

(g ∘ f)(-1)

Solution:

(g ∘ f)(-1) = g[f(-1)]

= g(1)

g[f(-1)]= -5

Problem 5 :

Use the graphs to evaluate the composition of functions.

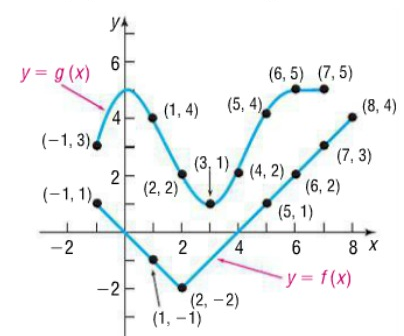
a) (g ∘ f)(1)      b) (g ∘ f)(5)      c) (f ∘ g)(0)    d) (f ∘ g)(2)

Solution:

a) (g ∘ f)(1)

From the graphs given above, it is clear that the line is crossing the curve f(x) at -1.

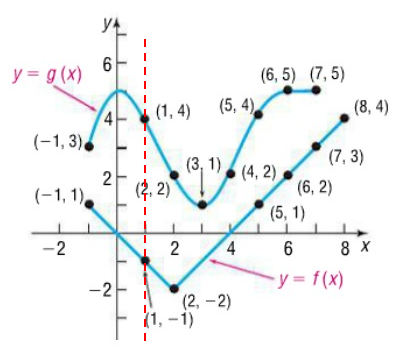
The value of f(1) is -1.

g(f(1)) = g(-1)

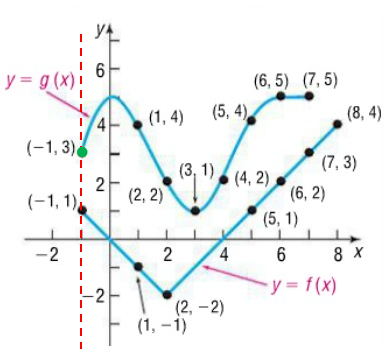
When x = -1, the vertical line crosses the curve g(-1) at 3.

g(f(1)) = 3

b) (g ∘ f)(5)

Solution:

From the graphs given above, it is clear that the line is crossing the curve f(x) at 1.

The value of f(5) is 1.

g(f(5)) = g(1)

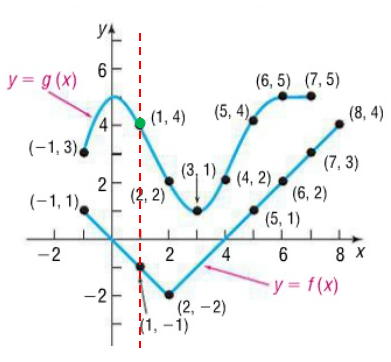
When x = 1, the vertical line crosses the curve g(1) at 4.

g(f(5)) = 4

c) (f ∘ g)(0)

Solution:

(f ∘ g)(0) = f[g(0)]

= f(5)

f[g(0)]= 1

d) (f ∘ g)(2)

Solution:

(f ∘ g)(2) = f[g(2)]

= f(2)

f[g(2)]= -2

Problem 6 :

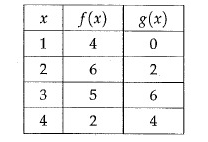
Four values for the functions f and g are shown in the table above. If g(m) = 6, what is the value of f(m) ?

Solution:

g(m) = 6

For what value of m, we find the value 6 in the function g(x).

m = 3

f(x) = f(3)

f(3) = 5

f(m) = f(3) = 5

Problem 7 :

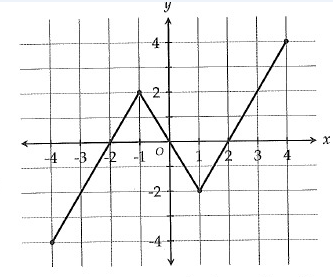
The function f is graphed in the xy-plane above. If f(c) = f(3), which of the following could be the value of c?

A) -3        B) -2        C) -1        D) 2

Solution:

From the given graph,

We have, f(c) = f(3)

f(3) = 2 (From the graph)

f(-1) = 2

f(3) = f(-1)

c = -1

So, option (C) is correct.

Problem 8 :

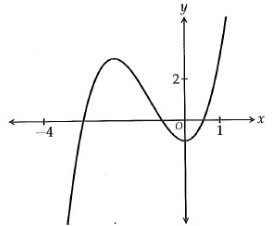
The graph of the function f in the xy-plane is shown above. For how many values of x in the portion of the graph shown above does f(x) = 2 ?

A) None    B) One    C) Two    D) Three

Solution:

Given, f(x) = 2 or y = 2

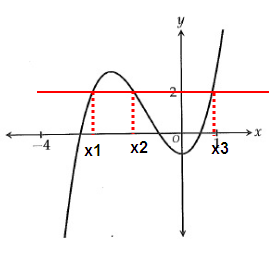
The horizontal line drawn at the point y = 2 crosses the curve at 3 places.

Hence, number of x value is three.

So, option (D) is correct.

Problem 9 :

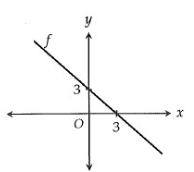
The function f is graphed in the xy-plane above. If the function g is defined by g(x) = f(x) + 2, what is the x-intercept of g(x)?

A) -1        B) 0       C) 1          D) 5

Solution:

y = mx + b

Slope m = -3/3

m = -1

f(x) = -x + 3

Adding 2 to get the equation of g(x) = -x + 3 + 2

g(x) = -x + 5

g(x) = 0

-x + 5 = 0

x = 5

So, option (D) is correct.

Problem 10 :

If f(x) = 3x - 1 and 2f(b) = 28, what is the value of f(2b)?

Solution:

Given, f(x) = 3x - 1

2f(b) = 28

x = b

f(b) = 3b - 1

2f(b) = 3b - 1

28 = 2(3b - 1)

28 = 6b - 2

30 = 6b

b = 5

f(2b) = f(2(5)) = f(10)

f(10) = 3(10) - 1

f(10) = 30 - 1 = 29

f(2b) = 29

Problem 11 :

f(x) = x² - 3x

g(x) = 2x + 14

The functions f and g are defined above. For how many values of k is it rue that f(k) = g(k)?

A) None        B) One      C) Two        D) More than two

Solution:

Given,

f(x) = x² - 3x

g(x) = 2x + 14

x = k

k² - 3k = 2k + 14

k² - 3k - 2k - 14 = 0

k² - 5k - 14 = 0

(k - 7) (k + 2) = 0

k = 7 or k = -2

k = 7

So, option (D) is correct.

Problem 12 :

The values in the table above define a linear function. What is the value of m + n?

A) -4      B) 0     C) 4           D) 8

Solution:

f(x) = ax + b

f(6) = 6a + b and f(5) = 5a + b

f(6) + f(5) = 6a + b + 5a + b

= 11a + 2b

We know,

f(4) = m and f(7) = n

m = 4a + b, n = 7a + b

m + n = 4a + b + 7a + b

m + n = 11a + 2b

m + n = f(5) + f(6)

f(5) + f(6) = 2 + (-2) = 0

m + n = f(5) + f(6) = 0

So, option (B) is correct.

Problem 13 :

A function f(x) has two properties;

f(a + b) = f(a) - b

f(2) = 10

What is the value of f(5)?

A) 5         B) 7          C) 9         D) 11

Solution:

According to f(2x) = 10

When x = 1

f(2x) = f(2) = 10

When b = 3 and a = 2

f(2 + 3) = f(2) - 3

= 10 - 3

= 7

So, option (B) is correct.