EQUATIONS OF PROPORTIONAL RELATIONSHIPS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
To find equations of proportional relationships, we have to follow the steps given below.
Step 1 :
Determine the constant of proportionality or unit rate for the problem by evaluating the ratio, y/x and assign that value to the variable k.
Step 2 :
Determine the independent and dependent variable for the problem. The independent variable is the variable x , and the dependent variable is the variable y
Step 3 :
Put in the form, y = kx
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Problem 1 :
A person who weighs 100 pounds to Earth weight 16.6 lb on the moon.
a) What is the independent variable ?
b) What is an equation that relates weight on Earth to weight of the moon ?
c) How much would be a 185 pound astronaut weight on the moon ?
d) How much would a man that weight 50 pounds on the moon weight on Earth ?
Solution :
Let E be the weight of object in Earth.
Let M be the weight of object in Moon.
a) Weight in Earth is independent, because based of an object on Moon is calculated based on the weight of an object in Earth.
b) Constant of proportionality :
100 pounds in earth = 16.6 lb in moon
1 pound in earth = 16.6/100 in moon
Constant of proportionality (k) = 16.6/100
M = (16.6/100) E
c) Weight of astronaut in earth = 185 pounds
M = 0.166 (185)
M = 30.71 lb
d) Weight in moon = 50 pounds
M = 0.166 E
When M = 50, E = ?
50 = 0.166 E
E = 50/0.166
E = 301.20 pounds
Problem 2 :
Write an equation that will model the proportional relationship given in each graph below and explain what the equation means in a statement.
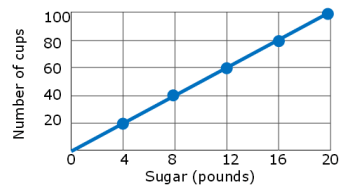
Solution :
Quantity of sugar in pounds (x) = independent variable
Number of cups (y) = Dependent variable
Using 4 pounds of sugar, we can make 20 cups.
1 pound of sugar = 20/4
= 5 cups
y = 5x
Problem 3 :
In 25 minutes Li can run 10 laps around the track. Consider the number of laps she can run per minute.
a. Find the constant of proportionality in this situation. What does it mean for this situation?
b. Write an equation to represent the relationship.
Solution :
a) Time taken (x) = independent variable
Number of laps done (y) = Dependent variable
25 minutes = 10 laps
1 minute = 10/25 laps
= 2/5
Meaning :
Per minute, he can run 2/5 of lap.
b) Constant of proportionality (k) = 2/5
y = (2/5) x
Problem 4 :
Bananas are $0.59/pound.
a. What is the constant of proportionality?
b. What is the equation that models the relationship between total price for bananas?
c. How much does 25 pounds of bananas cost?
Solution :
a) Constant of proportionality = 0.59
b) Let x be the quantity of bananas in pounds
let y be the cost of bananas.
y = 0.59 x
c) Applying x = 25 pounds
\y = 0.59(25)
y = 14.75
So, cost of 25 pounds of bananas is $14.75
Problem 5 :
The dry cleaning fee for 3 pairs of pants is $18.
a. What is the constant of proportionality?
b. What is the equation that models the relationship between total price for dry cleaning pants?
c. How much will the dry cleaner charge for 11 pairs of pants?
Solution :
Pair of pants (x) = independent variable
Cleaning fee (y) = Dependent variable
3 pairs of pants = $18
Cost of 1 pair of pant = 18/3
= $6
a) Constant of proportionality = $6
b) y = 6x
c) When x = 11
y = 6(11)
y = $66
Problem 6 :
Andrea is a street artist in New Orleans. She draws caricatures (cartoon-like portraits of tourists). People have their portrait drawn and then come back later to pick it up from her. The graph below shows the relationship between the number of portraits she draws and the amount of time in hours needed to draw the portraits.
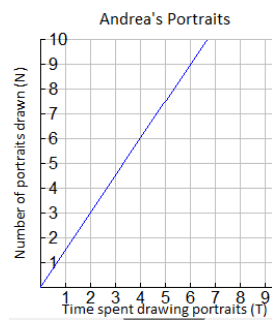
a) Write several ordered pairs from the graph and explain what each coordinate pair means in the context of this graph.
b) Determine the constant of proportionality and explain what it means in this situation.
c) Write an equation that will model the proportional relationship given in each real world situation.
Solution :
a) Some of the points are (2, 4) (4, 6) and (6, 9).
- In 2 hours 4 portraits drawn.
- In 4 hours 6 portraits drawn.
- In 6 hours 9 portraits drawn.
b) Number of hours (x) = Independent variable
number of portraits (y) = dependent variable
Constant of proportionality (k) = 4/2
k = 2
c) y = 2x
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling