EQUATIONS AND LINEAR FUNCTIONS PRACTICE EOC

Problem 1 :

If 8x = -4(x + 3), then x = ?

A)  -1     B)  1        C) 3/4     D)  1/4

Solution :

8x = -4(x + 3)

8x = -4x - 12

8x + 4x = -12

12x = -12

x = -12/12

x = -1

Problem 2 :

Solve for x :

9x² - c = d

Solution :

9x² - c = d

Adding c on both sides

9x² = d + c

Dividing by 9 on both sides.

x² = (d + c)/9

x = √[(d + c)/9]

x = √(d + c)/3

So, option A is correct.

Problem 3 :

Which inequality is represented by the graph below.

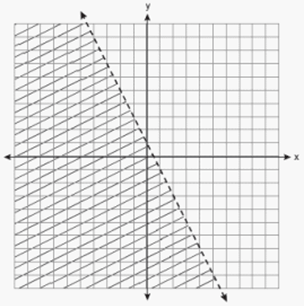
Solution :

Since it is the falling line, rise = 2 and run = 1

Slope = rise / run = 2

y-intercept = 1

y = 2x + 1

Choosing a point below the line (-1, 0),

0 = 2(-1) + 1

0 = -2 + 1

0 = -1

The line given is a dotted line, we should use dotted line.

y > 2x + 1

Problem 4 :

Jared can run 520 yards in one minute. How fast does he run in feet per second?

A)  12         B)  26              C)  1560          D)  16

Solution :

He can run 520 yards in one minute

3 ft = 1 yard

520 yard = 520(3)

= 1560 ft

In one minute, he can run 1560 ft.

1 minute = 60 seconds

60 second = 1560 ft

1 second = 1560/60

1 second = 26 ft

Problem 5 :

There are three consecutive integers such that the sum of the two smallest integers is 17 less than three times the largest. What is the smallest integer?

A)  5             B)  7                  C)  12                D)  6

Solution :

Let x, x + 1 and x + 2 be three consecutive integers.

x + x + 1 = 3(x + 2) - 17

2x + 1 = 3x + 6 - 17

2x - 3x = -17 + 6 - 1

-x = -12

x = 12

So, the smallest integer is 12.

Problem 6 :

Which expression is equivalent 

Solution :

Problem 7 :

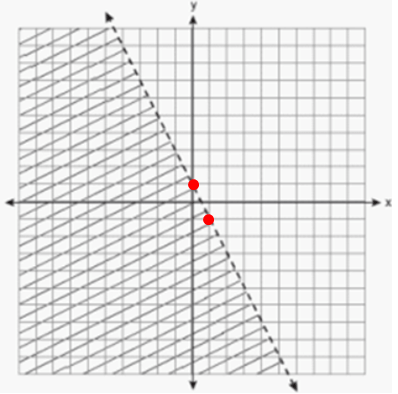
Which graph below displays the equation 3x - 4y = 28

Solution :

3x - 4y = 28

Finding x and y -intercepts, we get

In option A, the line has x-intercept is positive and y-intercept is negative.

So, option A is correct.

Problem 8 :

Compare the slope of f(x) = -2x + 3 and the slope of the chart of g(x) below.

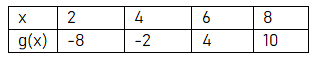
What is the positive difference between the slopes of f(x) and g(x)?

A)  1              B)  5                  C)  8                     D)  17

Solution :

Slope of g(x) from the table,

(2, -8) and (4, -2)

Slope (m) = [-2 - (-8)] / (4 - 2)

= (-2 + 8) / 2

= 6/2

= 3

f(x) = -2x + 3

Comparing with y = mx + b

Slope of f(x) = -2, slope of g(x) = 3. slope of g(x) is greater.

f(x) - g(x) = -2 - 3 ==> -5

Problem 9 :

Gregory teaches martial arts. He charges a one-time processing fee of $5.00 and the cost of the classes is shown below. Let x represent the number of classes and y represent the cost of classes.

Based on this information, what will it cost to take 10 classes?

A) $123        B)  $128          C)  $118           D)  $153

Solution :

(1, 15) and (2, 27)

Rate of change = (27 - 15) / (2 - 1)

= 12/1

= 12

y-intercept (initial cost) = 5

y = 12x + 5

Cost for 10 classes :

y = 12(10) + 5

y = 120 + 5

y = 125

Problem 10 :

Jerami is going to deposit an equal amount of money into a checking account each month until he has saved $2,000. The amount of money, y, in the account after x months can be modeled by the equation y = 35x + 250.

What does the slope of the graph of the equation represent?

[A] The amount of money deposited monthly

[B] The amount of money originally in the account

[C] The number of months it would take to earn $250

[D] The number of months it would take to reach $2,000

Solution :

Slope means rate of change, the amount he saves monthly. So, option A is correct.

Problem 11 :

Find the range of the function represented in the graph.

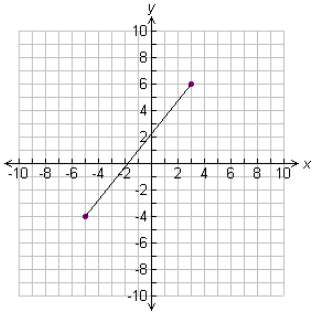
A)  The range consists of values from -5 to 3.

B)  The range consists of values from -4 to 6.

C)  The range consists of values from -5 to 6.

D) The range consists of values from -4 to 3.

Solution :

By observing the graph, the graph spread vertically in between -5 to 3.

Problem 12 :

Which equation represents the line passing through the points (3, 2) and (–9, 6)?

A) x – 3y = 9            B) x + 3y = 9

C) 3x – y = -9          D) 3x + y = 9

Solution :

(3, 2) and (–9, 6)

Slope (m) = (6 - 2) / (-9 - 3)

= -4/12

= -1/3

Equation of the line :

y - y₁ = m(x - x₁)

y - 2 = (-1/3) (x - 3)

3(y - 2) = -1(x - 3)

3y - 6 = -x + 3

x + 3y = 3 + 6

x + 3y = 9

Problem 13 :

Which of the following represents the linear equation

3(x + 2) = 12 – 2y

in standard form?

A) y = -3/2x + 3       B) y = 3/2x - 3    C) 3x – 2y = 10

D) 3x + 2y = 6

Solution :

3(x + 2) = 12 – 2y

3x + 6 = 12 - 2y

3x + 2y = 12 - 6

3x + 2y =6

2y = 6 - 3x

y = -3x/2 + 6/2

y = -3x/2 + 3