EQUATION PRACTICE WITH ANGLE ADDITION
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
To solve problems in this topic, we have to analyze the following.
Check the relationship between the angles involving.
Complementary and Supplementary
(i) If they are complementary to each other, they will add upto 90.
(ii) If they are supplementary, they will add upto 180.
About Triangles
(i) In triangle, sum of interior angle is 180.
(ii) In triangle, the exterior angle is equal to sum of remote interior angles.
Parallel Lines and Transversal
When two lines are parallel and they cut by the transversal, the following pairs will be congruent.
- Corresponding angles
- Alternate interior angles
- Alternate exterior angles
- Vertically opposite angles will be equal.
Sum of consecutive interior angles on the same side of the transversal will be equal to 180 degree.
Example 1 :
Find the value of x.
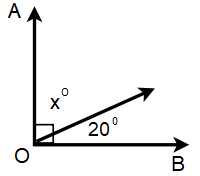
Solution :
By observing AOB, it is complementary. So, sum of the angles is 90.
x + 20 = 90
Subtracting 20 on both sides, we get
x = 90 - 20
x = 70
Example 2 :
Find x.
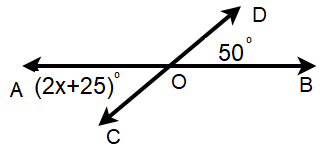
Solution :
∠AOC = ∠BOD (Vertically opposite angles)
2x + 25 = 50
Subtracting 25 on both sides, we get
2x = 50 - 25
2x = 25
Dividing by 2 on both sides.
x = 25/2
x = 12.5
Example 3 :
Find x.
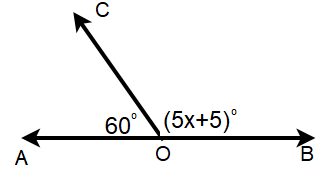
Solution :
AOB is a straight line. Its angle measure is 180.
∠AOC + ∠BOC = 180
60 + 5x + 5 = 180
5x + 65 = 180
Subtracting 65.
5x = 180 - 65
5x = 115
Divide by 5.
x = 115/5
x = 23
Example 4 :
Find x.
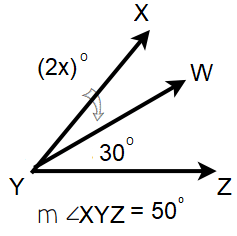
Solution :
∠XYZ = ∠XYW + ∠WYZ
50 = 2x + 30
Subtracting 30.
2x = 50 - 30
2x = 20
Dividing by 2.
x = 20/2
x = 10
Example 5 :
Find x.
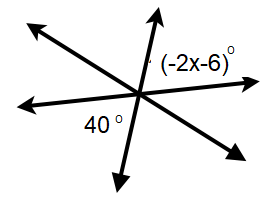
Solution :
By observing the picture given above, they are vertically opposite angles.
-2x - 6 = 40
Adding 6 on both sides.
-2x = 40 + 6
-2x = 46
Dividing by -2 on both sides.
x = 46/(-2)
x = -23
Example 6 :
Find the value of x.
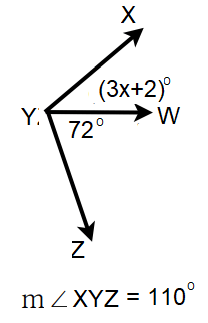
Solution :
∠XYW = 3x + 2
∠WYZ = 72
∠XYZ = 110
∠XYW + ∠WYZ = ∠XYZ
3x + 2 + 72 = 110
3x + 74 = 110
Subtracting 74 on both sides.
3x = 110 - 74
3x = 36
Dividing by 3 on both sides.
x = 36/3
x = 12
Example 7 :
Find the angle B.
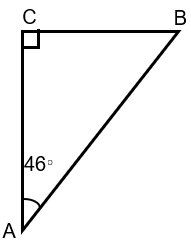
Solution :
In triangle ABC,
∠A + ∠B + ∠C = 180
Here ∠C = 90, ∠A = 46
46 + ∠B + 90 = 180
136 + ∠B = 180
∠B = 180 - 136
∠B = 44
Example 8 :
Find ∠JKX
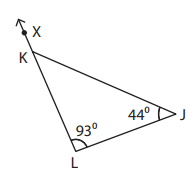
Solution :
Using exterior angle theorem.
∠JKX = ∠KLJ + ∠LJK
∠JKX = 93 + 44
∠JKX = 137
Example 9 :
Find the value of x.
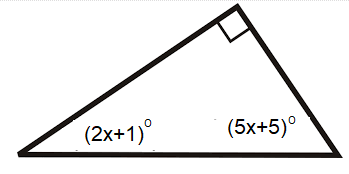
Solution :
In the triangle, the sum of interior angles is 180.
2x + 1 + 5x + 5 + 90 = 180
By combining the like terms, we get
7x + 96 = 180
Subtracting 96 on both sides.
7x = 180 - 96
7x = 84
Dividing by 7 on both sides.
x = 84/7
x = 12
Example 10 :
Find the value of x and y.
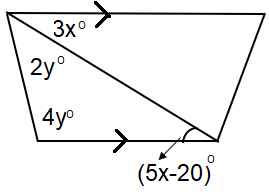
Solution :
From the picture, the opposite sides are parallel.
So, 3x and 5x-20 are alternate angles.
3x = 5x - 20
-2x = -20
x = 10
Sum of interior angle of triangle = 180
2y + 4y + 5x - 20 = 180
6y + 5x - 20 = 180
Add 20 on both sides.
6y + 5x = 180 + 20
6y + 5x = 200 -------(1)
Applying the value of x in (1)
6y + 5(10) = 200
6y + 50 = 200
By subtracting 50 on both sides.
6y = 200 - 50
6y = 150
Dividing by 6 on both sides, we get
y = 150/6
y = 25
Example 11 :
The angle x in the following figure
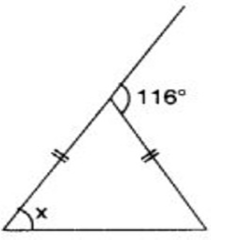
(a) 58° (b) 59° (c) 57° (d) 56˚
Solution :
The triangle given is a isosceles triangle.
Sum of remote interior angle = exterior angle
x + x = 116
2x = 116
x = 116/2
x = 58
So, option a is correct.
Example 12 :
In the following figure, find x if BA || CE.
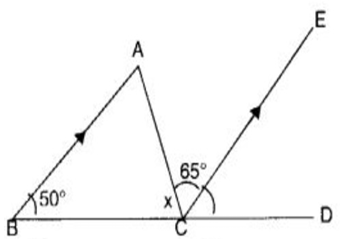
(a) 60° (b) 40° (c) 45° (d) 65°
Solution :
Given that BA and CE are parallel.
<ECD = 50
x + 65 + 50 = 180
x + 115 = 180
x = 180 - 115
x = 65
So, the value of x is 65. Option d is correct.
Example 13 :
Two angles of a triangle are of measures 75˚ and 35˚. Find the measures of the third angle.
Solution :
Let x be the third angle.
Sum of interior angles = 180
x + 75 + 35 = 180
x + 110 = 180
x = 180 - 110
x = 70
So, the missing angle is 70.
Example 14 :
Each of the two equal angles of a triangle is twice the third angle. Find the angles of the triangle.
Solution :
Let x be the third angle
2x be the other two angles.
2x + 2x + x = 180
5x = 180
x = 180/5
x = 36
2x = 2(36) ==> 72
So, the required angles are 36, 72 and 72.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling