EQUATION OF VERTICAL ASYMPTOTE WORKSHEET

Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.

Describe the vertical asymptotes and holes for the graph of each rational function.

Problem 1 :

y = (x - 2)/(x + 2) (x - 2)

Solution

Problem 2 :

y = x/x(x - 1)

Solution

Problem 3 :

y = (5 - x)/(x2 - 1)

Solution

Problem 4 :

y = (x2 - 2)/(x + 2)

Solution

Problem 5 :

y = (x2 - 4)/(x2 + 4)

Solution

Problem 6 :

y = (x + 3)/(x2 - 9)

Solution

Problem 7 :

y = (x2 - 25)/(x – 4)

Solution

Problem 8 :

y = (x - 2) (2x + 3)/(5x + 4) (x – 3)

Solution

Problem 9 :

y = (15x2 - 7x - 2)/(x2 - 4)

Solution

Answer Key

1)  Vertical asymptote at x = -2; hole at x = 2

2)  Vertical asymptote at x = 1; hole at x = 0

3)  Vertical asymptotes at x = 1 and x = -1

4)  Vertical asymptote at x = -2

5)  No vertical asymptotes and no holes

6)  Vertical asymptote at x = 3; hole at x = -3

7)  Vertical asymptote at x = 4

8)  Vertical asymptotes at x = -4/5 and x = 3.

9)  Vertical asymptotes at x = 2 and x = -2.

Problem 1 :

y = 2/(x – 6)

Solution

Problem 2 :

y = (x + 2)/(x – 4)

Solution

Problem 3 :

y = (x + 3)/2(x + 4)

Solution

Problem 4 :

y = (2x2 + 3)/(x2 – 6)

Solution

Problem 5 :

y = (3x - 12)/(x2 – 2)

Solution

Problem 6 :

y = (3x3 – 4x + 2)/(2x3 + 3)

Solution

For each function, determine the equations of any vertical asymptotes, the locations of any holes, and the existence of any horizontal or oblique asymptotes.

Problem 7 :

y = x/(x + 4)

Solution

Problem 8 :

y = 1/(x - 5) (x + 3)

Solution

Problem 9 :

y = (x + 4) / (x2 - 16)

Solution

Problem 10 :

Consider the function

f(x) = 3/(x - 2)

a) State the equation of the vertical asymptote.

b) Use a table of values to determine the behaviour(s) of the function near its vertical asymptote.

c) State the equation of the horizontal asymptote. 

d) Use a table of values to determine the end behaviours of the function near its horizontal asymptote.

e) Determine the domain and range.

f ) Determine the positive and negative intervals.

g) Sketch the graph.

Solution

Answer Key

1)  equation of the horizontal asymptote is y = 0 which is the x – axis.

2) equation of the horizontal asymptote is y = 1.

3)  equation of the horizontal asymptote is y = 1/2.

4)  equation of the horizontal asymptote is y = 2.

5)  equation of the horizontal asymptote is y = 0 which is the x – axis.

6) equation of the horizontal asymptote is y = 1.5.

7) 

Then y = 1 is the horizontal asymptote.

Equation of vertical asymptote is at x = -4

 there is no hole.

8) 

  • There is no hole.
  • Vertical asymptotes are at x = 5 and x = -3.
  • x-axis or y = 0 is the horizontal asymptote.

9) 

  • Vertical asymptote is at x = 4
  • Equation of horizontal asymptote y = 1

a) The vertical asymptote is at x = 2

b) The intervals are (-∞, 2) and (2, ∞)

  • When x ∈ (-∞, 2), f(x) will be negative. That is, when x < 2, f(x) is negative.
  • When x ∈ (2, ∞), f(x) will be positive. That is, when x > 2, f(x) is positive.

y-intercept is -3/2.

c) Highest exponent of the numerator = 0, highest exponent of the denominator = 1

Equation of horizontal asymptote is x-axis or y = 0.

d) End behavior :

  • x --> -∞ then f(x) --> 0
  • x --> ∞ then f(x) --> 0

e) Domain is all real numbers except x = 2

Range is all real values except y = 0

f) 

  • x ∈ (-∞, 2), f(x) will be negative
  • x ∈ (2, ∞), f(x) will be positive
eq-of-horizontal-asymptote-q1

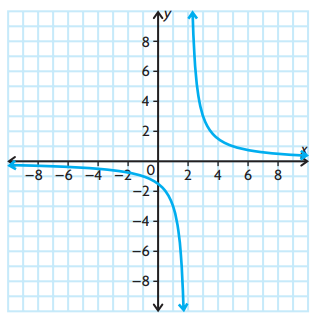
Describe the vertical asymptotes and holes for the graph of each rational function.

Problem 1 :

y = (x - 2)/(x - 2)(x + 2)

Solution

Problem 2 :

y = x/x(x - 1)

Solution

Problem 3 :

y = (5 - x) / (x2 - 1)

Solution

Problem 4 :

y = (x2 - 2)/(x + 2)

Solution

Problem 5 :

y = (x2 - 4)/(x2 + 4)

Solution

Problem 6 :

y = (x + 3)/(x2 - 9)

Solution

Problem 7 :

y = (x2 - 25) / (x - 4)

Solution

Problem 8 :

y = (x - 2)(2x + 3) / (5x + 4)(x - 3)

Solution

Problem 9 :

y = (15x2 - 7x - 2) / (x2 - 4) 

Solution

Problem 10 :

Suppose you start a home business typing technical research papers for college students. You must spend $3500 to replace your computer system. Then you estimate the cost of typing each page will be $0.02.

a. Write a rational function modeling your average cost per page. Graph the function.

b. How many pages must you type to bring your average cost per page to less than $1.50 per page, the amount you plan to charge?

Solution

Answer Key

1) vertical asymptotes are x = -2 and x = 2, hole at x = 2.

2) vertical asymptotes are x = 0 and x = 1, hole at x = 0.

3) vertical asymptotes are x = 1 and x = -1, no hole

4) vertical asymptote is x = -2, no hole

5)  no asymptote, no hole

6) vertical asymptotes are x = -3 and x = 3, hole at x = -3.

7) vertical asymptote is x = 4, no hole

8) vertical asymptotes are x = -4/5 and x = 3, no hole

9)  vertical asymptotes are x = 2 and x = -2, no hole

10) a)

123.png

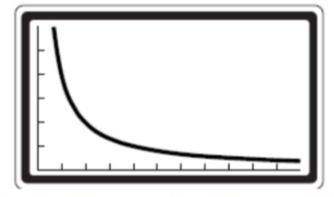
b) x = 2365

Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.

Recent Articles

RSS

  1. Finding Range of Values Inequality Problems

    May 21, 24 08:51 PM

    Finding Range of Values Inequality Problems

    Read More

  2. Solving Two Step Inequality Word Problems

    May 21, 24 08:51 AM

    Solving Two Step Inequality Word Problems

    Read More

  3. Exponential Function Context and Data Modeling

    May 20, 24 10:45 PM

    Exponential Function Context and Data Modeling

    Read More