EQUATION OF THE LINE THAT PASSES THROUGH THE POINTS

Example 1 :

Write an equation of the line that passes through the given points.

(-1, 3), (2, 9)

Solution :

Finding slope of the line passes through the above points :

Equation of the line :

y = mx + b ---(1)

Applying any one of the points given, say (-1, 3)

3 = 2(-1) + b

3 = -2 + b

b = 3 + 2

b = 5

Applying the slope and y-intercept in (1)

y = 2x + 5

Problem 2 :

Write an equation of the line that passes through the given points.

 (3, 7), (3, 5)

Solution :

Finding slope of the line passes through the above points :

Equation of the line :

(y - y₁) = m(x - x₁)

Applying any one of the points given, say (3, 7)

(y - 7) = (2/0)(x - 3)

Multiplying by 0 on both side

0 = x - 3

So, the required equation is x - 3 = 0.

Problem 3 :

If a line contains the points (0, 0) and (12, 16) then the line will also contain which of the following points ?

A)  (2, 3)      B)  (3, 2)     C)  (3, 4)      D)  (4, 3)

Solution :

Slope of the line which passes through any of the two points will be equal.

Figuring out the slope the line from the given points, we get

(0, 0) and (12, 16)

Checking whether we receive the same slope by taking one of the points from the question and options.

Option A :

So, (2, 3) is not one of the points lies on the line. Similarly option B will not work.

Option C :

So, (3, 4) is one of the points on the straight line.

Problem 4 :

In the xy-plane above, a point (not shown) with coordinates (t, t + 5)) lies on the line represented by y = f(z). What is the value of t ?

A)  -10     B) -5/2    C)  5     D)  5/2

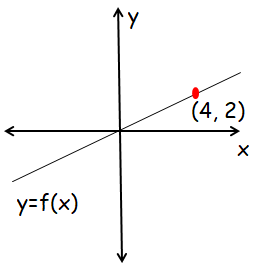
Solution :

From the figure, we observe the line passes through origin. So, the slope of the line shown above will be 2/4, that is 1/2.

Finding slope of the line by selecting any of the two points lies on the line will be equal.

Selecting the points (t, t + 5)) and (4, 2), we should receive 3/4.

So, the answer is option A.

Problem 5:

Find the y-intercept of the line which passes through the points (5, -2) and (1, 3).

Solution :

Finding slope of the line passes through two points (5, -2) and (1, 3).

Applying the slope in the formula y = mx + b

y = (-5/4) x + b

Applying any one of the points say (1, 3), we can solve for b

3 = (-5/4)(1) + b

3 + (5/4) = b

b = (12+5)/4

b = 17/4

So, the required y-intercept is 17/4. 

Problem 6 :

The equation of the perpendicular bisector of the segment joining the points whose coordinates are (1, 4) and (-2, 3) is

Solution :

The line perpendicular bisector will divide the line segment joining the points (1, 4) and (-2, 3) into two equal parts.

midpoint of the line segment = One of the points lies on the line

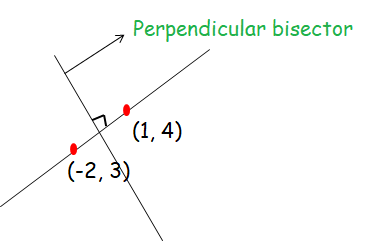
Slope of the line passes through the given points :

Slope of the perpendicular bisector = -3

Midpoint of the line segment :

Equation of the perpendicular bisector :

Problem 7 :

The function is graphed in the xy-plane below. If the function g is defined by g(x) = f(x) + 2. What is the x-intercept of g (x) ?

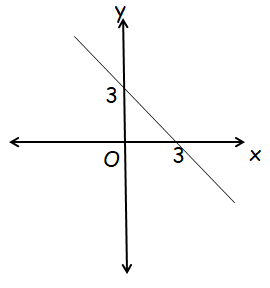
Solution :

Slope of the line = Rise / run

Since it is falling line, it will have negative slope.

Slope (m) = -3/3 ==> -1

y-intercept = 3

Equation of the line shown f(x) :

y = m x + b

y = -x + 3

g(x) = -x + 3 + 2

g(x) = -x + 5

To find x-intercept, we put y = 0 or g(x) = 0

-x + 5 = 0

x = 5

So, the required in the x-intercept is 5.