EQUATION OF TANGENT FOR THE CIRCLE WITHOUT DERIVATIVE

If the point of contact between a circle and a tangent is known, then the equation of the tangent can be calculated.

If a line is a tangent to a circle, then a radius will meet the tangent at right angles. The gradient of this radius can be calculated, since the center and point of contact are known.

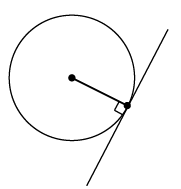
Using radius tangent

m _radius × m _tangent = −1

the gradient of the tangent can be found.

The equation can then be found using

y − y₁ = m(x − x₁)

since the point is known, and the gradient has just been calculated.

Problem 1 :

Show that  A (1, 3) lies on the circle x² + y² + 6x + 2y − 22 = 0 and find the equation of the tangent at A.

Solution :

To show that the given point lies on the circle, let us apply the point into the equation of circle.

If x = 1 and y = 3

1² + 3² + 6(1) + 2(3) − 22 = 0

1 + 9 + 6 + 6 - 22 = 0

22 - 22 = 0

0 = 0

Since the given point satisfies the equation of the circle, the point must lie on the circle.

Finding center of the circle :

x² + y² + 6x + 2y − 22 = 0

x² + 6x + y² + 2y − 22 = 0

(x + 3)² + (y + 1)² - 3² - 1² - 22 = 0

(x + 3)² + (y + 1)² = 32

Center of the circle is (-3, -1).

Slope of radius from (-3, -1) and (1, 3) :

m = (y₂ - y₁)/(x₂ - x₁)

m = (3+1)/(1+3)

m = 4/4

m = 1

Slope of tangent = -1/Slope of radius

= -1

Equation of tangent :

(y - y₁) = m(x - x₁)

Equation of the tangent at the point (1, 3).

y - 3 = -1(x - 1)

y - 3 = -x + 1

x + y = 1 + 3

x + y = 4

So, equation of tangent for the given circle is x + y = 4.

Problem 2 :

Find the equation of the tangent to the circle

x² + y² - 3x + y - 10 = 0

through the point R (-1, 2) on its circumference.

Solution :

x² + y² - 3x + y - 10 = 0

Finding center of the circle :

x² - 3x + y²+ y - 10 = 0

(x - 3/2)² - (3/2)² + (y + 1/2)² - (1/2)² - 10 = 0

(x - 3/2)² + (y + 1/2)² - (9/4) - (1/4) - 10 = 0

(x - 3/2)² + (y + 1/2)² = (50/4)

Center (3/2, -1/2)

Slope of the radius from (3/2, -1/2) and R(-1, 2) :

m = (2 + 1/2)/(-1 - 3/2)

m = (5/2) / (-5/2)

m = -1

Slope of the tangent = -1/(-1) ==> 1

Equation of the tangent line :

Point (-1, 2) and slope = 1

y - 2 = 1(x + 1)

y - 2 = x + 1

x - y = -2 - 1

x - y = -3

Problem 3 :

Find the equation of tangent to the circle

x² + y² + 4x + 6y - 5 = 0

from the point R(1, 6) on its circumference.

Solution :

x² + y² + 4x + 6y - 5 = 0

Finding center of the circle :

x² + 4x + y² + 6y - 5 = 0

(x + 2)² + (y + 3)² - 2² - 3² - 5 = 0

(x + 2)² + (y + 3)² = 18

Center (-2, -3)

Slope of the radius from (-2, -3) and R(1, 6) :

m = (6 + 3)/(1 + 2)

m = 9 / 3

m = 3

Slope of the tangent = -1/3

Equation of the tangent line :

Point (1, 6) and slope = 1/3

y - 6 = (1/3)(x - 1)

3(y - 6) = x - 1

3y - 18 = x - 1

x - 3y = -18 + 1

x - 3y = -17

So, equation of the tangent is x - 3y = -17.