EQUATION OF TANGENT AND NORMAL TO THE CURVE

Tangent is also a line which touches the curve. To find the equation of tangent, we have to follow the given below.

i) Find the slope of the tangent drawn at the point (x₁, y₁) from the given equation of curve.

Use the formula,

y - y₁ = m(x - x₁)

ii)  Here m is the slope of the tangent line at the point of contact. (x₁, y₁) is the point of contact.

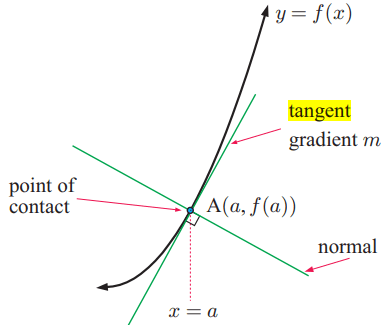
Normal is line the perpendicular to tangent line drawn at the point of contact.

We use the formula 

y - y₁ = m(x - x₁)

Find the equation of tangent and normal to the curve at the given point.

Problem 1 :

y = x – 2x² + 3 at x = 2

Solution :

y = x – 2x² + 3 at x = 2

When, x = 2, then

So, the required point is (2, -3).

Equation of tangent :

(y - y₁) = m(x - x₁)

(y + 3) = -7(x - 2)

y + 3  = -7(x - 2)

y + 3 = -7x + 14

7x + y + 3 - 14 = 0

7x + y - 11 = 0

Equation of normal :

(y - y₁) = (-1/m)(x - x₁)

(y + 3) = 1/7(x - 2)

7(y + 3) = 1(x - 2)

7y + 21 = x - 2

x - 2 - 7y - 21 = 0

x - 7y - 23 = 0

Problem 2 :

y = √x + 1 at x = 4

Solution :

y = √x + 1 at x = 4

When, x = 4, then 

So, the required point is (4, 3).

Equation of tangent :

(y - y₁) = m(x - x₁)

(y - 3) = 1/4(x - 4)

4(y - 3)  = x - 4

4y - 12 = x - 4

x - 4y + 12 - 4 = 0

x - 4y + 8 = 0

Equation of normal :

(y - y₁) = (-1/m)(x - x₁)

(y - 3) = -4(x - 4)

y - 3 = -4x + 16

4x + y - 3 - 16 = 0

4x + y - 19 = 0

Problem 3 :

y = x³ - 5x at x = 1

Solution :

y = x³ - 5x at x = 1

When, x = 1, then 

So, the required point is (1, -4).

Equation of tangent :

(y - y₁) = m(x - x₁)

(y + 4) = -2(x - 1)

y + 4  = -2x + 2

2x + y + 4 - 2 = 0

2x + y + 2 = 0

Equation of normal :

(y - y₁) = (-1/m)(x - x₁)

(y + 4) = (-1/-2)(x - 1)

(y + 4) = (1/2)(x - 1)

2(y + 4) = x - 1

2y + 8 = x - 1

x - 2y - 8 - 1

x - 2y - 9 = 0

Problem 4 :

y = 4/√x at (1, 4)

Solution :

y = 4/√x at (1, 4)

dy/dx = -2/(√x)³

= -2/(√1)³

= -2/√1

= -2/1

Slope (m) = -2

So, the required point is (1, 4).

Equation of tangent :

(y - y₁) = m(x - x₁)

(y - 4) = -2(x - 1)

y - 4  = -2x + 2

2x + y - 4 - 2 = 0

2x + y - 6 = 0

Equation of normal :

(y - y₁) = (-1/m)(x - x₁)

(y - 4) = (-1/-2)(x - 1)

(y - 4) = (1/2)(x - 1)

2(y - 4) = 1(x - 1)

2y - 8 = x - 1

x - 2y + 8 - 1 = 0

x - 2y + 7 = 0

Problem 5 :

Solution :

So, the required point is (-1, -4).

Equation of tangent :

(y - y₁) = m(x - x₁)

(y + 4) = -5(x + 1)

y + 4  = -5x - 5

5x + y + 4 + 5 = 0

5x + y + 9 = 0

Equation of normal :

(y - y₁) = (-1/m)(x - x₁)

(y + 4) = (-1/-5)(x - 1)

(y + 4) = (1/5)(x - 1)

5(y + 4) = 1(x - 1)

5y + 20 = x - 1

x - 5y - 20 - 1 = 0

x - 5y - 21 = 0

Problem 6 :

y = 3x² - 1/x at x = -1.

Solution :

y = 3x² - 1/x at x = -1.

When, x = -1

So, the required point is (-1, 4).

Equation of tangent :

(y - y₁) = m(x - x₁)

(y - 4) = -5(x + 1)

y - 4  = -5x - 5

5x + y - 4 + 5 = 0

5x + y + 1 = 0

Equation of normal :

(y - y₁) = (-1/m) (x - x₁)

(y - 4) = (-1/-5)(x + 1)

-5(y - 4) = -1(x + 1)

-5y + 20 = -x - 1

x - 5y + 20 + 1 = 0

x - 5y + 21 = 0