EQUATION OF PARABOLA WITH VERTEX AND FOCUS WORKSHEET

Find the equation of the parabola that satisfies the given conditions.

Problem 1 :

Vertex (0, 0) and focus (0, -2)

Problem 2 :

Vertex (3, 2) and focus (3, 6)

Problem 3 :

Find the vertex and focus of the parabola.

(y - 2)² + 16(x - 3) = 0

Problem 4 :

Find the standard form of the equation of the parabola with the given characteristic and vertex at the origin. focus: (0, 7)

Problem 5 :

Find the equation of the parabola with vertex at (5, 4) and focus at (-3, 4).

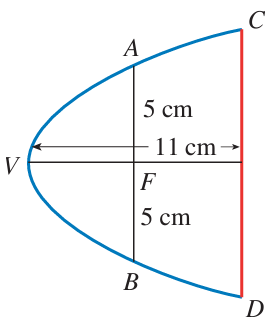
Problem 6 :

A cross section of a parabolic reflector is shown in the figure. The bulb is located at the focus and the opening at the focus is 10 cm.

a) Find the equation of parabola

b) Find the diameter of the opening |CD|, 11 cm from the vertex.

Find the equation of the parabola. Then find focus and directrix.

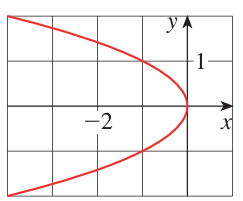
Problem 7 :

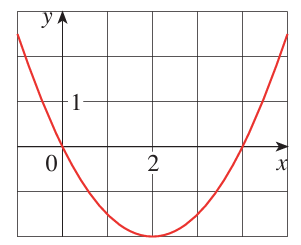
Problem 8 :

Answer Key

1) the required equation of parabola is y² = 8x.

2) the required equation of parabola is (y - 2)² = 16(x - 3)

3) (y - 2)² = 16(x - 3)

4) the required equation will be y² = 28x.

5) the required equation of parabola is (y - 5)² = 32(x - 4)

6) the diameter is 20.96 cm.

7) y² = -x, Focus ==> (-1/4, 0)

Equation of directrix ==> x = 1/4

8) (x - 2)² = 2(y + 2), Focus ==> (2, -3/2)

Equation of directrix ==> y = -5/2