EQUATION OF LINE AND SLOPE PRACTICE PROBLMES SAT

Problem 1 :

A line in the xy-plane passes through the origin and has a slope of 1/7 . Which of the following points lies on the line?

a) (0, 7)    b) (1, 7)     c) (7, 7)     d) (14, 2)

Solution :

One of the points on the straight line is origin (0, 0).

Slope = 1/7

Slope of the line joining the points

Slope (m) = (y₂ - y₁) / (x₂ - x₁)

So, the point (14, 2) lies on the line.

Problem 2 :

In the xy-plane above, line A is parallel to line k. What is the value of p ?

a) 4     b) 5     c) 8     d) 10

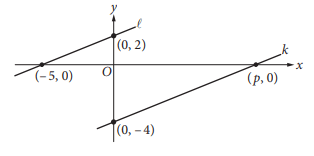
Solution :

Slope of the line joining the points (-5, 0) and (0, 2)

m = (2 - 0) / (0 - (-5))

= 2/5 -----(1)

Slope of the line joining the points (0, -4) and (p, 0)

m = (0 - (-4)) / (p - 0)

= (0 + 4) / p

= 4/p -----(2)

Since the lines are parallel, their slopes will be equal.

(1) = (2)

2/5 = 4/p

2p = 5(4)

2p = 20

p = 10

So, the answer is option d.

Problem 3 :

The graph of a line in the xy-plane has slope 2 and contains the point (1, 8). The graph of a second line passes through the points (1, 2) and (2, 1). If the two lines intersect at the point (a, b), what is the value of a + b ?

a) 4       b) 3      c) −1       d) −4

Solution :

Equation of the first line :

Slope = 2, Point (1, 8)

y - y₁ = m(x - x₁)

y - 8 = 2(x - 1)

y = 2x - 2 + 8

y = 2x + 6 -----(1)

Equation of second line :

(1, 2) and (2, 1)

Slope = (y₂ - y₁) / (x₂ - x₁)

= (1 - 2) / (2 - 1)

= -1

(y - 2) = -1 (x - 1)

y - 2 = -1x + 1

y = -1x + 1 + 2

y = -x + 3 -----(2)

(1) = (2)

2x + 6 = -x + 3

2x + x = 3 - 6

3x = -3

x = -1

Applying the value of x in (1), we get

y = -(-1) + 3

y = 4

Problem 4 :

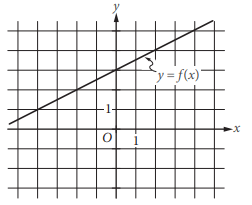
The graph of the linear function f is shown in the xy-plane above. The slope of the graph of the linear function g is 4 times the slope of the graph of f. If the graph of g passes through the point (0, −4) , what is the value of g(9) ?

a) 5     b) 9    c) 14     d) 18

Solution :

Slope of line f :

(0, 3) and (2, 4) are the points lie on the line

slope = (4 - 3) / (2 - 0)

= 1/2

Slope of linear function g = 4 (1/2) = 2

Line g passes through the point (0, -4)

y - (-4) = 2(x - 0)

y + 4 = 2x

y = 2x - 4

g(x) = 2x - 4

g(9) = 2(9) - 4

= 14

So, option c is correct.

Problem 5 :

Line A in the xy-plane contains points from each of Quadrants II, III, and IV, but no points from Quadrant I. Which of the following must be true?

a) The slope of line A is undefined.

b) The slope of line A is zero.

c) The slope of line A is positive.

d) The slope of line A is negative

Solution :

It must be a falling line, then its slope will be negative.

Problem 6 :

In the xy-plane, the line determined by the points (2, k)  and (k, 32) passes through the origin. Which of the following could be the value of k ?

a) 0         b) 4       c) 8       d) 16

Solution :

(2, k) (k, 32) and (0, 0) lies on the same line.

If the points are collinear, then 

(1) = (2)

(32 - k) / (k - 2) =  32/k

k(32 - k) = 32(k - 2)

32k - k² = 32k - 64

k² + 32k - 32k - 64 = 0

k² - 64 = 0

(k - 8) (k + 8) = 0

k = 8 and k = -8

So, the value of k is 8.

Problem 8 :

What are the slope and y-intercept of the line 

5x + 4y + 3 = 0?

Solution :

5x + 4y + 3 = 0

4y = -5x - 3

Dividing by 4 on both sides,

y = -5x/4 - (3/4)

Slope m = -5/4 and y-intercept = -3/4

Problem 9 :

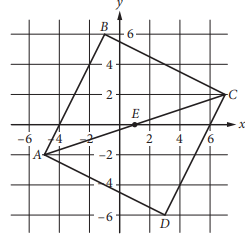
In the xy-plane above, ABCD is a square and point E is the center of the square. The coordinates of points C and E are (7, 2) and (1, 0), respectively. Which of the following is an equation of the line that passes through points B and D ?

a) y = −3x − 1     b) y = −3(x − 1)

c) y = (−1/3)x + 4    d) y = − (1/3)x − 1

Solution :

The shape shown above is a square, then the diagonals will be perpendicular to each other.

Finding slope of line passes through the points C and E :

m = (0 - 2) / (1 - 7)

= -2/(-6)

= 1/3

Slope of the line passes through B which is perpendicular to the other diagonal :

= -3

Equation of the line :

y - 0 = -3(x - 1)

y = -3(x - 1)

So, option b is correct.

Problem 10 :

−2x + 3y = 6

In the xy-plane, the graph of which of the following equations is perpendicular to the graph of the equation above?

a) 3x + 2y = 6    b) 3x + 4y = 6    c) 2x + 4y = 6

d) 2x + 6y = 3

Solution :

−2x + 3y = 6

If two lines are perpendicular, then the product of their slopes will be equal to -1.

Slope of the given line :

−2x + 3y = 6

3y = 2x + 6

y = (2/3)x + 2

Slope of the given line = 2/3

Option a :

3x + 2y = 6

2y = -3x + 6

y = (-3/2)x + 3

Slope of this line = -3/2

So, these two lines are perpendicular to each other.