EQUATION OF A LINE FROM A GRAPH

Problem 1 :

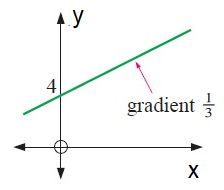
Solution :

Slope of a line = 1/3

y- Intercept (b) = 4

Equation of a straight line y = mx + b

M = 1/3t + 4

So, the required equation is M = 1/3t + 4

Problem 2 :

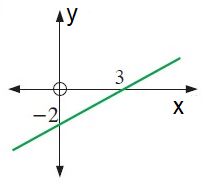
Solution:

x - intercept a = 3

N - intercept b = -2

By using x - intercept and y - intercept formula,

x/a + y/b = 1

x/3 + y(-2) = 1

x/3 - y/2 = 1

-y = -2/3x + 2

y = (2/3)x - 2

So, the required equation is y = (2/3)x - 2

Problem 3 :

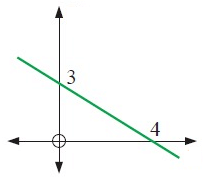
Solution :

x - intercept form a = 4

y - intercept form b = 3

By using x - intercept and y - intercept formula,

x/a + y/b = 1

x/4 + y/3 = 1

y/3 = -x/4 + 1

y = (-3/4)x + 3

So, the required equation is y = (-3/4)x + 3

Problem 4 :

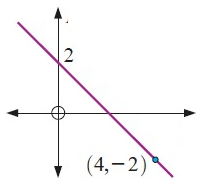
Solution :

In the figure given above, y-intercept is given and we have a point on the line.

(4, -2) and (0, 2)

m = (y₂ - y₁) / (x₂ - x₁)

m = (2 + 2) / (0 - 4)

m = -4/4

m = -1

Equation of the line :

y - y₁ = m(x - x₁)

y - 4 = -1(x + 2)

y - 4 = -x - 2

y = -x - 2 + 4

y = -x + 2

Problem 5 :

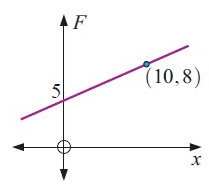
Solution :

In figure, the straight line passes through two points (10, 8) and (0, 5)

(10, 8) and (0, 5)

m = (y₂ - y₁) / (x₂ - x₁)

m = (5 - 8) / (0 - 10)

m = 3/10

Equation of the line :

y - y₁ = m(x - x₁)

y - 8 = (3/10)(x - 10)

10(y - 8) = 3(x - 10)

10y - 80 = -3x - 30

10y = -3x - 30 + 80

10y = -3x + 50

y = -(3/10)x + 5

Problem 6 :

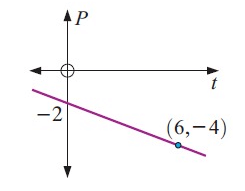
Solution :

In figure, the straight line passes through two points (6, -4) and (0, -2)

(6, -4) and (0, -2)

m = (y₂ - y₁) / (x₂ - x₁)

m = (2 + 4) / (0 - 6)

m = -6/6

m = -1

Equation of the line :

y - y₁ = m(x - x₁)

y + 4 = -1(x - 6)

y - 4 = -x + 6

y = -x + 6 + 4

y = -x + 10