EQUATION OF A CIRCLE WITH END POINTS OF DIAMETER

To find equation of the circle with endpoints of diameter, we use the formula given below.

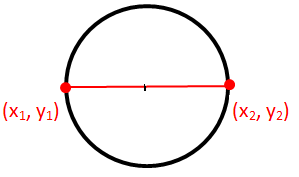
Equation of circle :

(x - x₁) (x - x₂) + (y - y₁) (y - y₂) = 0

Problem 1 :

Ends of a diameter : (-9, 5) and (1, 1)

Solution :

Now we have to consider the given points as (x₁, y₁) and (x₂, y₂). So the values of x₁ = -9, y₁ = 5, x₂ = 1 and y₂ = 1

Equation of circle :

(x - x₁) (x - x₂) + (y - y₁) (y - y₂) = 0

(x + 9) (x - 1) + (y - 5) (y - 1) = 0

x² - x + 9x - 9 + y² - y - 5y + 5 = 0

x² + 8x - 4 + y² - 6y = 0

So, the required equation of a circle

x² + y² + 8x - 6y - 4 = 0

Problem 2 :

Ends of a diameter : (6, 8) and (16, 6)

Solution :

Here x₁ = 6, y₁ = 8, x₂ = 16 and y₂ = 6

Equation of circle :

(x - x₁) (x - x₂) + (y - y₁) (y - y₂) = 0

(x - 6) (x - 16) + (y - 8) (y - 6) = 0

x² - 16x - 6x + 96 + y² - 6y - 8y + 48 = 0

x² - 22x + 144 + y² - 14y = 0

So, the required equation of a circle

x² + y² - 22x - 14y + 144 = 0

Problem 3 :

Ends of a diameter : (19, 5) and (-5, 1)

Solution :

Here x₁ = 19, y₁ = 5, x₂ = -5 and y₂ = 1

(x - 19) (x + 5) + (y - 5) (y - 1) = 0

x² + 5x - 19x - 95 + y²  - y - 5y + 5 = 0

x² - 14x - 90 + y² - 6y = 0

So, the required equation of a circle 

x² + y² - 14x - 6y - 90 = 0

Problem 4 :

Ends of a diameter : (11, -5) and (11, -7)

Solution :

Here x₁ = 11, y₁ = -5, x₂ = 11 and y₂ = -7

(x - 11) (x - 11) + (y + 5) (y + 7) = 0

x²  - 11x  - 11x + 121 + y² + 7y + 5y  + 35 = 0

x² - 22x + 156 + y²  + 12y = 0

So, the required equation of a circle 

x² - 22x + 156 + y²  + 12y = 0.

Problem 5 :

Given a circle with (5, 1) and (3, -1) as the endpoints of the diameter.

Solution :

Here x₁ = 5, y₁ = 1, x₂ = 3 and y₂ = -1

(x - 5) (x - 3) + (y - 1) (y + 1) = 0

x² - 3x - 5x + 15 + y² + y - y - 1 = 0

x² - 8x + 14 + y² = 0

So, the required equation of a circle x² + y² - 8x + 14 = 0.

Problem 6 :

Given a circle with (2, 1) and (6, -3) as the endpoints of the diameter.

Solution :

Here x₁ = 2, y₁ = 1, x₂ = 6 and y₂ = -3

(x - 2) (x - 6) + (y - 1) (y + 3) = 0

x² - 6x - 2x + 12 + y² + 3y - y - 3 = 0

x² - 8x + 9 + y² + 2y = 0

So, the required equation of a circle 

x² + y² - 8x + 2y + 9 = 0.

Problem 7 :

Given a circle with (4, -3) and (2, 1) as the endpoints of the diameter.

Solution :

Here x₁ = 4, y₁ = -3, x₂ = 2 and y₂ = 1

(x - 4) (x - 2) + (y + 3) (y - 1) = 0

x² - 2x - 4x + 8 + y² - y + 3y - 3 = 0

x² - 6x + 5 + y² + 2y = 0

So, the required equation of a circle 

x² + y² - 6x + 2y + 5 = 0.