END BEHAVIOR OF A POLYNOMIAL FUNCTION WORKSHEET
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
The graphs of the following function are shown.
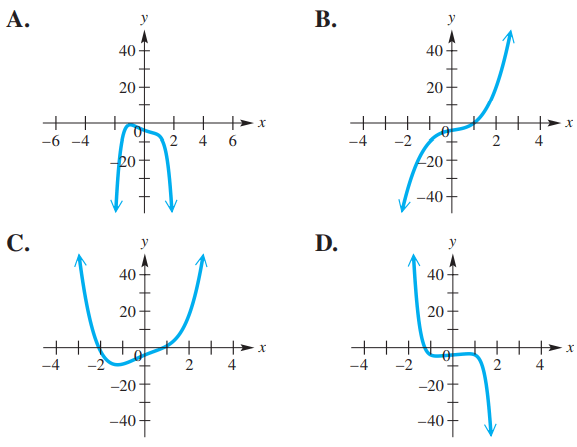
Problem 1 :
|
f(x) = x4 - x2 + 5x - 4 h(x) = 3x3 - x2 + 2x - 4 |
g(x) = -x6 + x2 - 3x - 4 k(x) = -x7 + x - 4 |
Match the function with its graph.
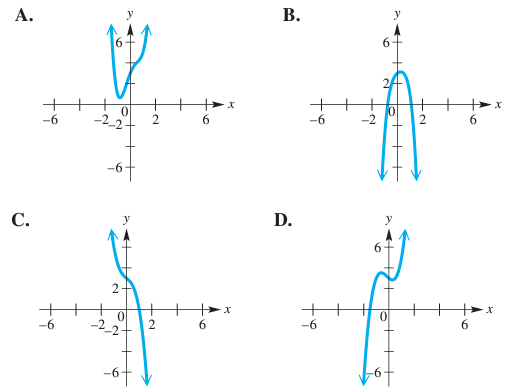
Problem 2 :
Without using a calculator, match each function with the correct graph in choices A–D.
|
f(x) = 2x3 + x2 - x + 3 g(x) = - 2x3 - x + 3 |
h(x) = -2x4 + x3 - 2x2 + x + 3 k(x) = 2x4 - x3 - 2x2 + 3x + 3 |
Answer Key
1)
f(x) = x4 - x2 + 5x - 4
Degree of the polynomial f(x) is 4, it is even.
a = 1 > 0
The function f(x) is even degree with positive leading coefficient on its dominating term. It exactly matches with graph C.
g(x) = -x6 + x2 - 3x - 4
Degree of the polynomial f(x) is 6, it is even.
a = -1 < 0, then as | x | -> ∞, P(x) -> -∞. Option A is correct.
h(x) = 3x3 - x2 + 2x - 4
h(x) is the polynomial of odd degree and a = 3 > 0
When x -> ∞, P(x) -> ∞ and as x -> -∞, P(x) -> -∞. So, option B is correct.
k(x) = -x7 + x - 4
h(x) is the polynomial of odd degree and a = -1 < 0
When | x | -> ∞, P(x) -> -∞. So, option D is correct.
2)
f(x) = 2x3 + x2 - x + 3
f(x) is the odd degree polynomial, here a = 2 > 0
When x -> ∞, P(x) -> ∞ and as x -> -∞, P(x) -> -∞. So, option D is correct.
g(x) = - 2x3 - x + 3
g(x) is the odd degree polynomial, here a = -2 < 0
When | x | -> ∞, P(x) -> -∞. So, option C is correct.
h(x) = -2x4 + x3 - 2x2 + x + 3
It is even degree polynomial. Here a = -2 < 0
When | x | -> ∞, P(x) -> -∞. So, option B is correct.
k(x) = 2x4 - x3 - 2x2 + 3x + 3
It is even degree polynomial. Here a = 2 > 0
When | x | -> ∞, P(x) -> ∞. So, option A is correct.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling