ELIMINATION METHOD WORKSHEET

Problem 1 :

x + 2y = 20

2x + y = 19

Problem 2 :

3x - 2y = -2

4x - 3y = -4

Problem 3 :

9x + 4y = 11

3x - 10y = -2

Problem 4 :

4x + 3y = 21

5x + 2y = 21

Problem 5 :

-3x - 5y = -7

-4x - 3y = -2

Problem 6 :

8x + 4y = 12

7x + 3y = 10

Problem 7 :

4x + 3y = -7

-2x - 5y = 7

Solution and Answers

1. Answer

x + 2y = 20 ---> (1)

2x + y = 19 ---> (2)

Comparing coefficients of x and y, 

Both x terms and y terms have different coefficients in the above system of equations.

Let's try to make the coefficients of y terms equal.

To make the coefficients of y terms equal, we have to find the least common multiple 2 and 1.

The least common multiple of 2 and 1 is 2.

Multiply the second equation by -2 in order to make the coefficient of y as -2.

(1) ---> x + 2y = 20

(2) ⋅ -2 ---> -4x - 2y = -38

Now, we can add the two equations and eliminate y as shown below. 

x = 6

Substitute 6 for x in (1).

6 + 2y = 20

2y = 14

y = 7

So, the values of x and y are 6 and 7 respectively.

2. Answer

3x - 2y = -2 ---> (1)

4x - 3y = -4 ---> (2)

The least common multiple of 2 and 3 is 6.

Multiply the first equation by -3 in order to make the coefficient of y as 6 and multiply the second equation by 2 in order to make the coefficient of y as -6.

(1) ⋅ -3 ---> -9x + 6y = 6

(2) ⋅ 2 ---> 8x - 6y = -8

Now, we can add the two equations and eliminate y as shown below. 

x = 2

Substitute 2 for x in (1).

3(2) - 2y = -2

6 - 2y = -2

-2y = -8

y = 4

So, the values of x and y are 2 and 4 respectively.

3. Answer

9x + 4y = 11 ---> (1)

3x - 10y = -2 ---> (2)

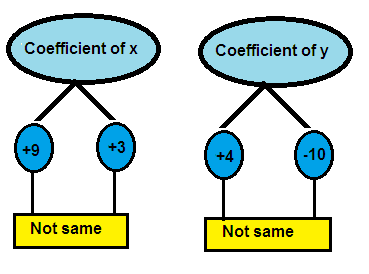
Both x terms and y terms have different coefficients in the above system of equations.

Let's try to make the coefficients of x terms equal.

To make the coefficients of x terms equal, we have to find the least common multiple 9 and 3.

The least common multiple of 9 and 3 is 9.

Multiply the second equation by -3 in order to make the coefficient of x as -9.

(1) ---> 9x + 4y = 11

(2) . -3 ---> -9x + 30y = 6

Now, we can add the two equations and eliminate x as shown below.

y = 17/34

y = 1/2

Substitute 1/2 for y in (1).

9x + 4(1/2) = 11

9x + 2 = 11

9x = 9

x = 1

So, the values of x and y are 1 and 1/2 respectively.

4. Answer

4x + 3y = 21 ---> (1)

5x + 2y = 21 ---> (2)

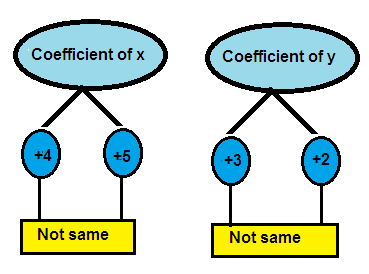
Both x terms and y terms have different coefficients in the above system of equations.

Let's try to make the coefficients of x terms equal.

To make the coefficients of y terms equal, we have to find the least common multiple 3 and 2.

The least common multiple of 3 and 2 is 6.

Multiply the first equation by 2 in order to make the coefficient of y as 6 and multiply the second equation by -3 in order to make the coefficient of y as -6.

(1) . 2 ---> 8x + 6y = 42

(2) . -3 ---> -15x - 6y = -63

Now, we can add the two equations and eliminate y as shown below.

x = 21/7

x = 3

Substitute 3 for x in (1).

4(3) + 3y = 21

12 + 3y = 21

3y = 9

y = 3

So, the values of x and y are 3 and 3 respectively.

5. Answer

-3x - 5y = -7 ---> (1)

-4x - 3y = -2 ---> (2)

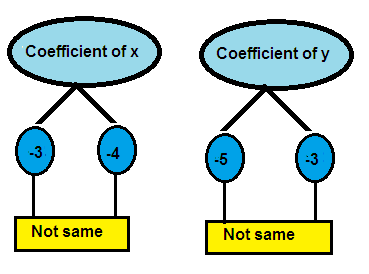
Both x terms and y terms have different coefficients in the above system of equations.

Let's try to make the coefficients of y terms equal.

To make the coefficients of y terms equal, we have to find the least common multiple 4 and 3.

The least common multiple of 4 and 3 is 12.

Multiply the first equation by 3 in order to make the coefficient of y as 12 and multiply the second equation by -4 in order to make the coefficient of y as -12.

(1) . 3 ---> 24x + 12y = 36

(2) . -4 ---> -28x - 12y = -40

Now, we can add the two equations and eliminate y as shown below.

x = 1

Substitute 1 for x in (1).

8(1) + 4y = 12

8 + 4y = 12

4y = 4

y = 1

So, the values of x and y are 1 and 1 respectively.

6. Answer

4x + 3y = -7 ---> (1)

-2x - 5y = 7 ---> (2)

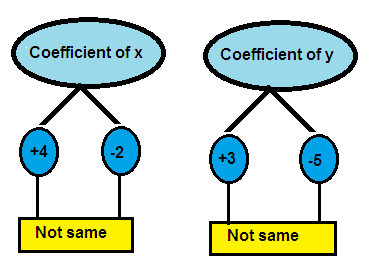
Both x terms and y terms have different coefficients in the above system of equations.

Let's try to make the coefficients of x terms equal.

To make the coefficients of x terms equal, we have to find the least common multiple 4 and 2.

The least common multiple of 4 and 2 is 4.

Multiply the second equation by 2 in order to make the coefficient of x as 4.

(1) ---> 4x + 3y = -7

(2) . 2 ---> -4x - 10y = 14

y = -1

Substitute -1 for y in (1).

4x + 3(-1) = -7

4x - 3 = -7

4x = -4

x = -1

So, the values of x and y are -1 and -1 respectively.