DRAW THE ANGLE IN STANDARD POSITION

Angles in standard position are always shown on the Cartesian plane. The x-axis and the y-axis divide the plane into four quadrants

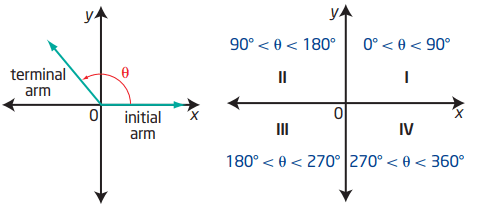
On a Cartesian plane, you can generate an angle by rotating a ray about the origin.

The starting position of the ray, along the positive x-axis, is the initial arm of the angle. The final position, after a rotation about the origin, is the terminal arm of the angle.

An angle is said to be an angle in standard position if its vertex is at the origin of a coordinate grid and its initial arm coincides with the positive x-axis.

Draw the angle with the given measure in standard position.

Problem 1 :

−340°

Solution :

-340°

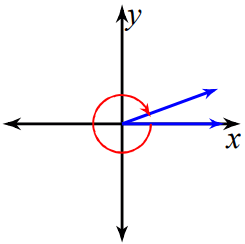
Moving clockwise rotation, should land at 1^st quadrant.

Problem 2 :

150°

Solution :

150°

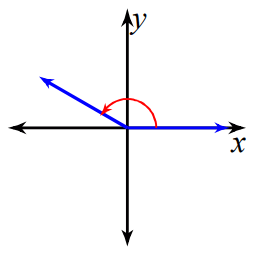
Moving clockwise rotation, should land at 2^nd quadrant.

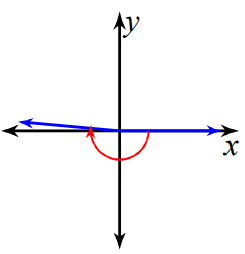
Problem 3 :

-185°

Solution :

-185°

Since the given angle is negative, we move in clock wise direction. The terminal side will lie on the 2^nd quadrant.

Problem 4 :

300°

Solution :

300°

Since the given angle is positive, we move in counter clock wise direction. The terminal side will lie on the 4^th quadrant.

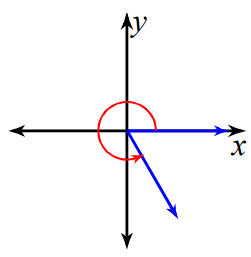
Problem 5 :

-260°

Solution :

-260°

Since the given angle is negative, we move in clock wise direction. The terminal side will lie on the 2^nd quadrant.

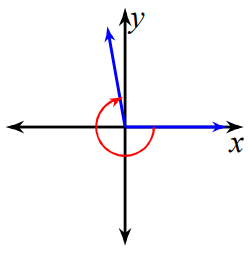
Problem 6 :

220°

Solution :

220°

Since the given angle is positive, we move in counter clock wise direction. The terminal side will lie on the 3^rd quadrant.

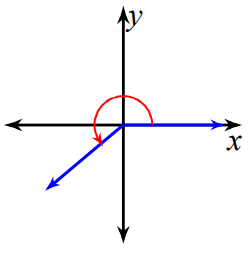
Find the measure of each principal angle.

Problem 7 :

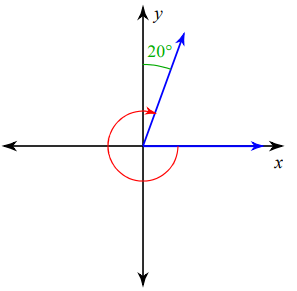
Solution :

Direction of rotation = clock wise rotation.

Angle should be negative and its terminal side is on the first quadrant.

- 270 - 20 = -290°

So, the required angle is -290°.

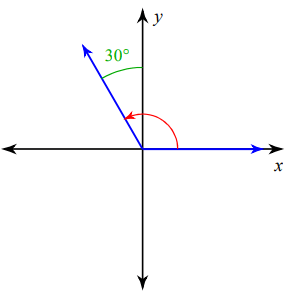
Problem 8 :

Solution :

Direction of rotation = counter clock wise rotation.

Angle should be positive and its terminal side is on the second quadrant.

90 + 30 = 120°

So, the required angle is 120°.

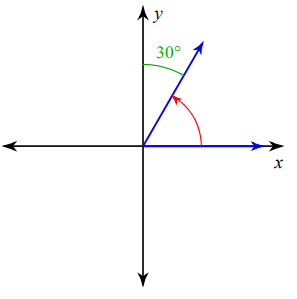
Problem 9 :

Solution :

Direction of rotation = counter clock wise rotation.

Angle should be positive and its terminal side is on the first  quadrant.

90 - 30 = 60°

So, the required angle is 60°.

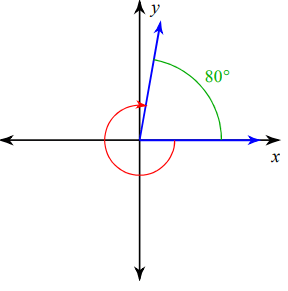
Problem 10 :

Solution :

Direction of rotation = clock wise rotation.

Angle should be negative and its terminal side is on the first  quadrant.

= -270 - (90 - 80)

= -270° - 90 + 80

= -280°

So, the required angle is -280°.

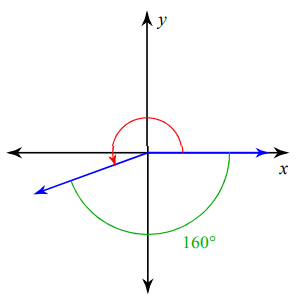
Problem 11 :

Solution :

Direction of rotation = clock wise rotation.

Angle should be positive and its terminal side is on the third  quadrant.

180 + 180 - 160 = 200°

So, the required angle is 200°.

Problem 12 :

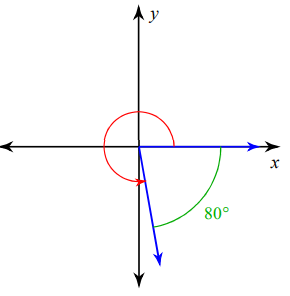
Solution :

Direction of rotation = counter clock wise rotation.

Angle should be positive and its terminal side is on the first  quadrant.

270 + 90 - 80 = 280°

So, the required angle is 280°.