DRAW BOX AND WISHKER PLOT FOR THE GIVEN DATA

To draw the box and whisker plot, we have to follow the instruction given below.

Step 1 :

Arrange the data from least to greatest

Step 2 :

Calculate the median(Q₂) which divides the data into two equal parts.

Step 3 :

• Calculate the lower quartile (Q₁) by finding the median of lower half.
• Calculate the upper quartile (Q₃) by finding the median of upper half.

Step 4 :

• Starting from the least value draw the tail and at least value start drawing box.

Problem 1 :

Draw a box and whisker plot for the data set:

12, 14, 14, 12, 16, 13, 11, 14, 18

Solution:

Let us write the observations in the data in ascending order.

11, 12, 12, 13, 14, 14, 14, 16, 18

Median is dividing the data set into two parts.

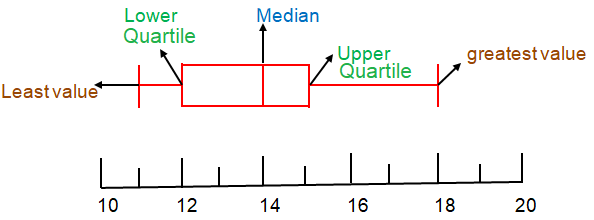
Lower quartile Q₁:

The data set is having four values. So,

Q₁ = (12 + 12) / 2

= 24/2

Q₁ = 12

Upper quartile Q₃:

The data set is having four values. So,

Q₃ = (14 + 16) / 2

= 30/2

Q₃ = 15

Median Q₂:

The median is the middle value in a set of data.

So, median Q₂ = 14

Problem 2 :

Draw a box and whisker plot for the data set:

16, 14, 13, 13, 18, 12, 11, 12, 12

Solution :

Let us write the observations in the data in ascending order.

11, 12, 12, 12, 13, 13, 14, 16, 18

Median is dividing the data set into two parts.

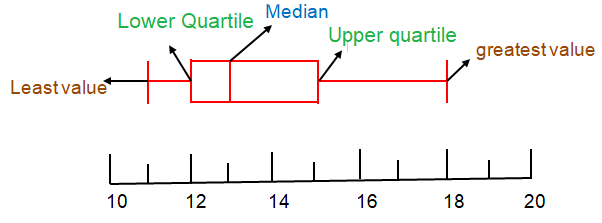
Median of lower half Q₁:

The data set is having four values. So,

Q₁ = (12 + 12) / 2

= 24/2

Q₁ = 12

Median of upper half Q₃:

The data set is having four values. So,

Q₃ = (14 + 16) / 2

= 30/2

Q₃ = 15

Median Q₂:

The median is the middle value in a set of data.

So, median Q₂ = 13

Problem 3:

Draw a box and whisker plot for the data set:

32, 34, 36, 37, 36, 37, 38, 37, 38

Solution :

Let us write the observations in the data in ascending order.

32, 34, 36, 36, 37, 37, 37, 38, 38

Median is dividing the data set into two parts.

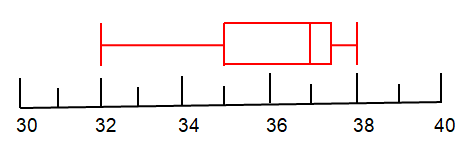
Median of lower half Q₁:

The data set is having four values. So,

Q₁ = (34 + 36) / 2

= 70/2

Q₁ = 35

Median of upper half Q₃:

The data set is having four values. So,

Q₃ = (37 + 38) / 2

= 75/2

                                                       Q₃ = 37.5    

Median Q₂:

The median is the middle value in a set of data.

So, median Q₂ = 37

Problem 4 :

Draw a box and whisker plot for the data set:

22, 24, 25, 26, 21, 22, 28, 29, 23

Solution :

Let us write the observations in the data in ascending order.

21, 22, 22, 23, 24, 25, 26, 28, 29

Median is dividing the data set into two parts.

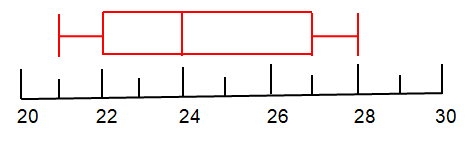
Median of lower half Q₁:

The data set is having four values. So,

Q₁ = (22 + 22) / 2

= 44/2

Q₁ = 22

Median of upper half Q₃:

The data set is having four values. So,

Q₃ = (26 + 28) / 2

= 54/2

                                                        Q₃ = 27      

Median Q₂:

The median is the middle value in a set of data.

So, median Q₂ = 24                  

Problem 5 :

Draw a box and whisker plot for the data set:

52, 52, 55, 55, 53, 56, 57, 57, 58

Solution :

Let us write the observations in the data in ascending order.

52, 52, 53, 55, 55, 56, 57, 57, 58

Median is dividing the data set into two parts.

Median of lower half Q₁:

The data set is having four values. So,

Q₁ = (52 + 53) / 2

= 105/2

Q₁ = 52.5

Median of upper half Q₃:

The data set is having four values. So,

Q₃ = (57 + 57) / 2

= 114/2

                                                        Q₃ = 57      

Median Q₂:

The median is the middle value in a set of data.

So, median Q₂ = 55                  

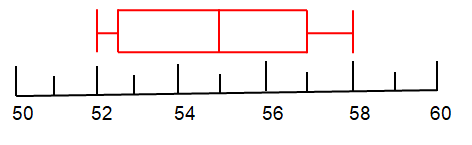
Problem 6 :

Draw a box and whisker plot for the data set:

34, 38, 34, 37, 32, 32, 39, 34, 39

Solution :

Let us write the observations in the data in ascending order.

32, 32, 34, 34, 34, 37, 38, 39, 39

Median is dividing the data set into two parts.

Median of lower half Q₁:

The data set is having four values. So,

Q₁ = (32 + 34) / 2

= 66/2

Q₁ = 33

Median of upper half Q₃:

The data set is having four values. So,

Q₃ = (38 + 39) / 2

= 77/2

 Q₃ = 38.5 

Median Q₂:

The median is the middle value in a set of data.

So, median Q₂ = 34

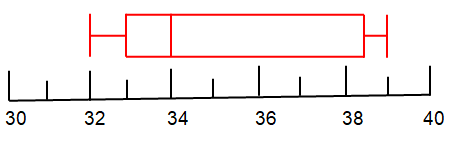
Problem 7 :

Draw a box and whisker plot for the data set:

50, 51, 52, 58, 58, 59, 49, 50, 49

Solution :

Let us write the observations in the data in ascending order.

49, 49, 50, 50, 51, 52, 58, 58, 59

Median is dividing the data set into two parts.

Median of lower half Q₁:

The data set is having four values. So,

Q₁ = (49 + 50) / 2

= 99/2

Q₁ = 49.5

Median of upper half Q₃:

The data set is having four values. So,

Q₃ = (58 + 58) / 2

= 116/2

Q₃ = 58      

Median Q₂:

The median is the middle value in a set of data.

So, median Q₂ = 51

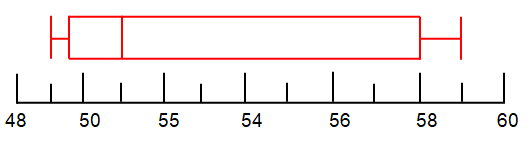
Problem 8 :

Draw a box and whisker plot for the data set:

37, 38, 36, 33, 34, 32, 34, 37, 32

Solution :

Let us write the observations in the data in ascending order.

32, 32, 33, 34, 34, 36, 37, 37, 38

Median is dividing the data set into two parts.

Median of lower half Q₁:

The data set is having four values. So,

Q₁ = (32 + 33) / 2

= 65/2

Q₁ = 32.5

Median of upper half Q₃:

The data set is having four values. So,

Q₃ = (37 + 37) / 2

= 74/2

                                                        Q₃ = 37    

Median Q₂:

The median is the middle value in a set of data.

So, median Q₂ = 34

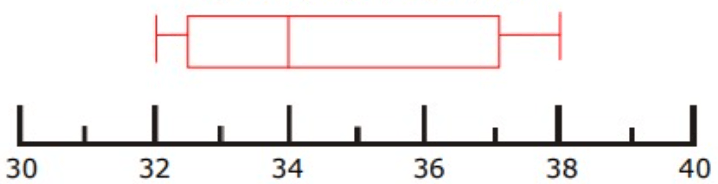
Problem 9 :

Draw a box and whisker plot for the data set:

18, 16, 15, 19, 11, 14, 12, 14, 16

Solution :

Let us write the observations in the data in ascending order.

11, 12, 14, 14, 15, 16, 16, 18, 19

Median is dividing the data set into two parts.

Median of lower half Q₁:

The data set is having four values. So,

Q₁ = (12 + 14) / 2

= 26/2

Q₁ = 13

Median of upper half Q₃:

The data set is having four values. So,

Q₃ = (16 + 18) / 2

= 34/2

                                                        Q₃ = 17    

Median Q₂:

The median is the middle value in a set of data.

So, median Q₂ = 15

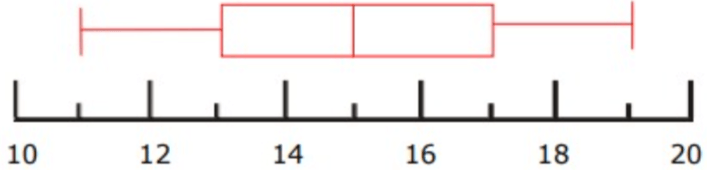
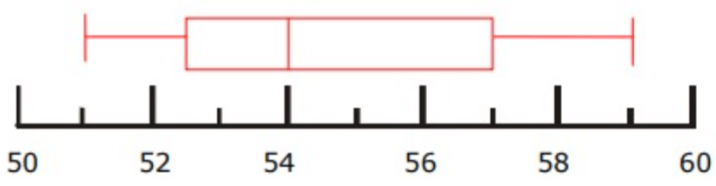
Problem 10 :

Draw a box and whisker plot for the data set:

55, 56, 58, 59, 54, 54, 51, 53, 52

Solution :

Let us write the observations in the data in ascending order.

51, 52, 53, 54, 54, 55, 56, 58, 59

Median is dividing the data set into two parts.

Median of lower half Q₁:

The data set is having four values. So,

Q₁ = (52 + 53) / 2

= 105/2

Q₁ = 52.5

Median of upper half Q₃:

The data set is having four values. So,

Q₃ = (56 + 58) / 2

= 114/2

Q₃ = 57    

Median Q₂:

The median is the middle value in a set of data.

So, median Q₂ = 54