DOMAIN RANGE VERTEX AND ZEROES OF QUADRATIC FUNCTION

Find the important information and sketch.

(i) Vertex form

(ii)  Max/Min

(iii) Axis of symmetry

(iv) Domain

(v) Range

(vi) Zeroes

(vii) y-intercept

Problem 1 :

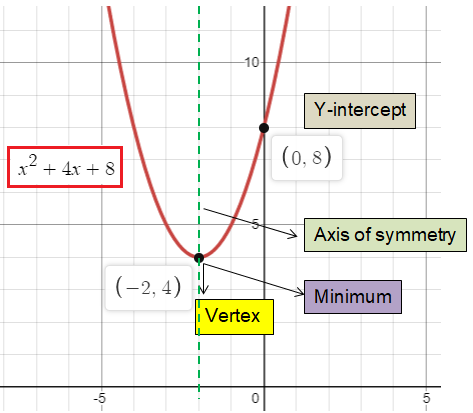
f(x) = x² + 4x + 8

Solution :

Let f(x) = y

y = x² + 4x + 8

(i) Vertex form :

Converting the equation into vertex for

y = a(x - h)² + k

Writing the coefficient of x as multiple of 2.

y = x² + 2 ⋅ x ⋅ 2 + 2² - 2² + 8

y = (x + 2)² - 2² + 8

y = (x + 2)² - 4 + 8

y = (x + 2)² + 4

(h, k) ==> (-2, 4)

(ii) Maximum / Minimum :

y = 1(x + 2)² + 4

Here a = 1 > 0, so the parabola opens up. 

The given quadratic function will have minimum value.

(iii)  Axis of symmetry :

x = -b/2a

f(x) = x² + 4x + 8

Comparing the given equation with y = ax² + bx + c

a = 1, b = 4 and c = 8

x = -4/2(1)

x = -2

(iv) Domain :

Domain of the function is -∞ < x < ∞

(v) Range :

Since the minimum value is 4, the curve will go below 4. So the range is y  ≥  4.

(vi) Zeroes :

x² + 4x + 8 = 0

Since this quadratic function is not factorable, we will check the nature of roots.

Nature of roots = b² - 4ac

= 42 - 4(1)(8)

= 16 - 32

= -16 < 0

So, the quadratic function has no real roots.

(vii) y-intercept :

y = x² + 4x + 8

To find y-intercept, put x = 0

y = 0² + 4(0) + 8

y = 8

So, the y-intercept is (0, 8).

Problem 2 :

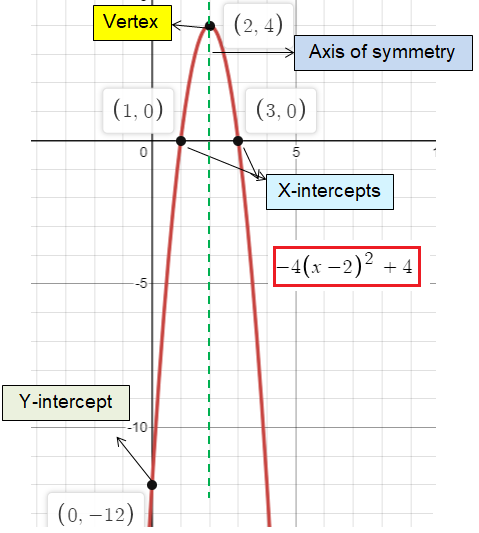
f(x) = -4(x - 2)² + 4

Solution :

(i) Vertex form :

The given questions is in vertex form.

y = -4(x - 2)² + 4

(h, k) ==> (2, 4)

(ii) Maximum / Minimum :

y = -4(x - 2)² + 4

Here a = -4< 0, so the parabola opens down. 

The given quadratic function will have maximum value.

(iii)  Axis of symmetry :

Axis of symmetry will be at vertex.

x = -2

(iv) Domain :

Domain of the function is -∞ < x < ∞

(v) Range :

Since the minimum value is 4, the curve will go below 4. So the range is y  ≥  4.

(vi) Zeroes :

 -4(x - 2)² + 4 = 0

 -4(x - 2)² = -4

(x - 2)² = 1

Taking square roots on both sides, we get

x - 2 = √1

x - 2 = ±1

x - 2 = 1 and x - 2 = -1

x = 1 + 2 and x = -1 + 2

x = 3 and x = 1

So, zeroes are 1 and 3.

(vii) y-intercept :

y =  -4(x - 2)² + 4

To find y-intercept, put x = 0

y =  -4(0 - 2)² + 4

y = -4(4) + 4

y = -16 + 4

y = -12

So, the y-intercept is (0, -12).