DOMAIN AND RANGE OF PIECEWISE FUNCTION
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Piecewise function will consist of more than one pieces. To find domain of the piecewise function, we have to find the domain of the pieces separately and find the union of all domains.
This can be done simply after we draw the graph of the given piecewise function.
How to find domain and range of piecewise function from graph ?
To find domain of piecewise function, we have to observe the graph horizontally. The places where we cannot see the graph, we have exclude those x-values from domain.
To find range of the function, we have to observe the graph vertically. The places where we cannot see the part of the graph, we have to exclude those y-values from range.
|
Linear function ax + by + c = 0 or y = mx + b |
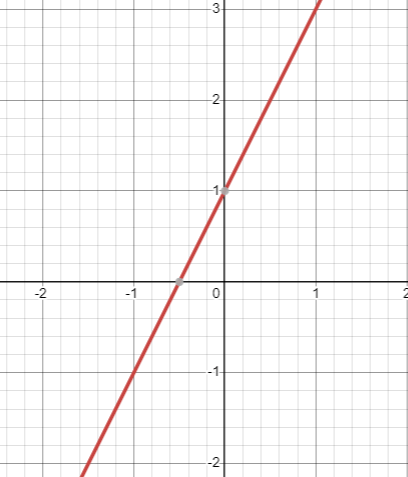 |
|
Horizontal line : y = k Vertical line : x = k |
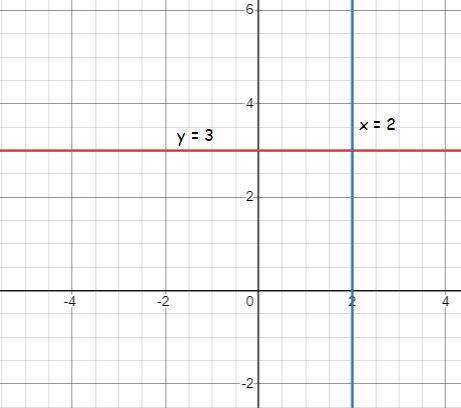 |
|
Quadratic function y = ax2 + bx + c or y = a(x-h)2 + k |
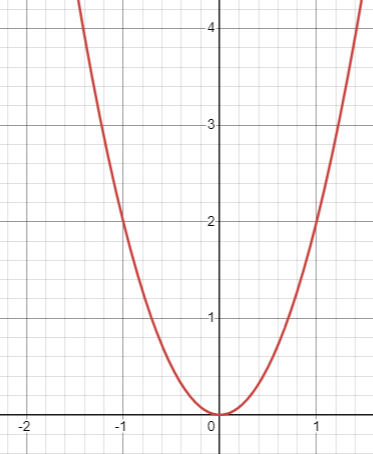 |
|
Absolute value function y = a |x - h| + k |
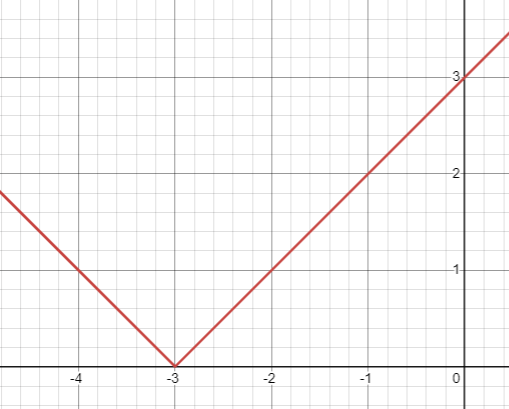 |
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Graph each piecewise function. Then, find the domain and range for each piecewise function.
Problem 1 :
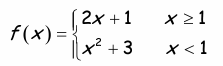
Solution :
First piece :
y = 2x + 1
Since it is in the form y = mx + b, it is a linear function.
The domain of this function is (-∞, 1].
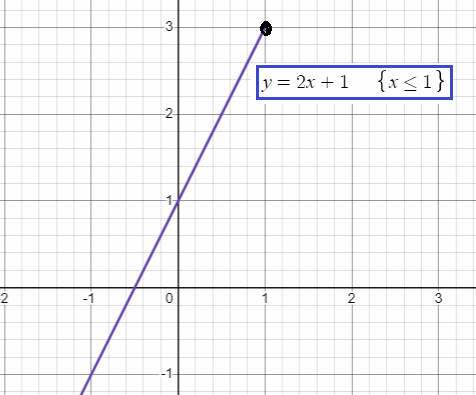
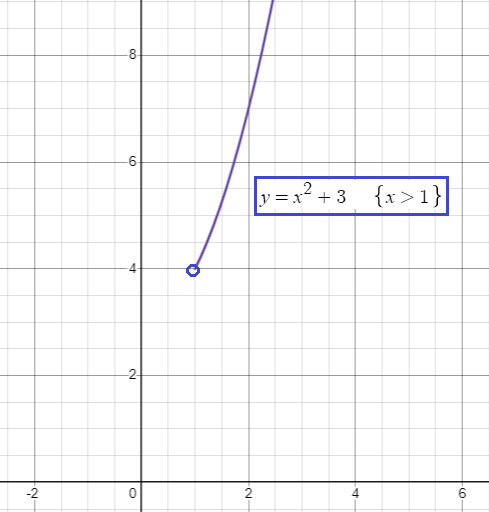
Second piece :
y = x2 + 3
Since it is in the form y = a(x - h)2 + b, it is a quadratic function.
The domain of this function is (1, ∞)
Connecting these two pieces in the single graph, we get
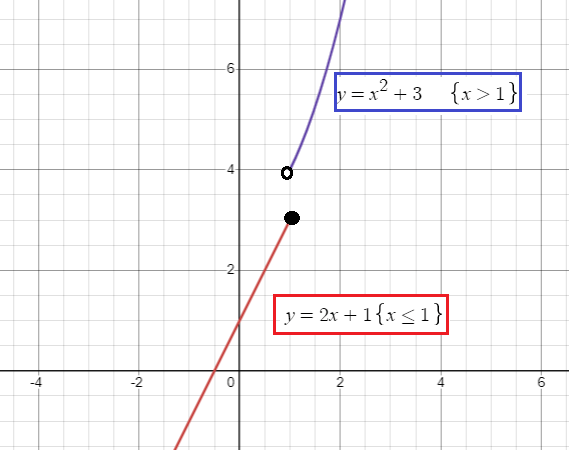
Observing the graph horizontally, we know that there is no break or gaps in the graph. So,
Domain of the given piecewise function is (-∞, ∞)
By observing the graph vertically, there is no gap vertically. Then the range is (-∞, ∞).
Problem 2 :
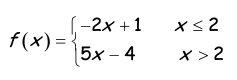
Solution :
Graph of first piece :
y = -2x + 1
The given function is a linear function which has the y-intercept as 1 and slope as -2. It must be a falling line.
Graphing second piece :
y = 5x - 4
It is also a line function which has the slope of 5 and y-intercept as -4. It must be a raising line.
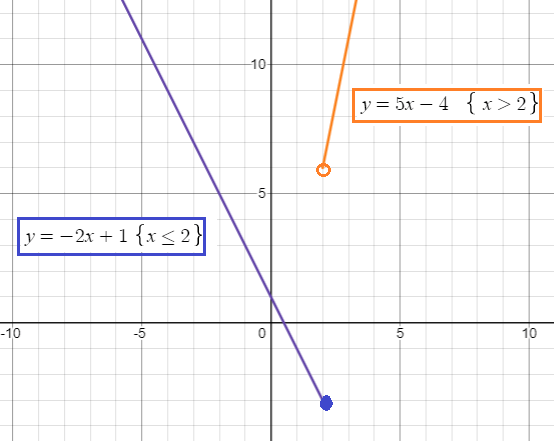
By observing the graph horizontally, the domain is (-∞, ∞) and the range is (-2, ∞).
Problem 3 :
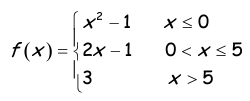
Solution :
Graph of first piece :
y = x2 - 1
The given function is a quadratic function. Using the concept of transformation, by moving down the graph of the parent function y = x2, we will get the graph of y = x2 - 1
The parabola will lie in the left of side of the vertical axis since x ≤ 1
Graphing second piece :
y = 2x - 1
Since it is a linear function, the graph will be a straight line. Slope is 2 and y-intercept is -1.
Graphing third piece :
y = 3
It is horizontal line passes through 3.
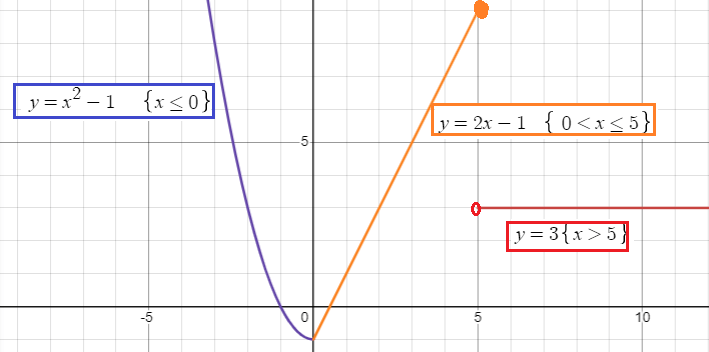
By observing the graph horizontally, the domain is (-∞, ∞) and the range is (-∞, ∞).
Problem 4 :
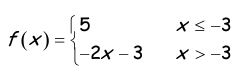
Solution :
Graph of first piece :
y = 5
It is the horizontal line passes through 5. We may draw the horizontal line up to x = -3, we cannot go to the right of -3.
Graphing second piece :
y = -2x - 3
It is linear function with slope of -2 and y-intercept of -3. It must be a falling line.
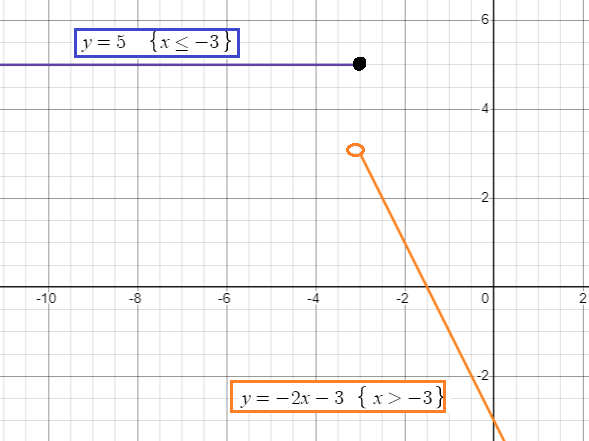
By observing the graph horizontally, the domain is (-∞, ∞) and the range is (-∞, 3) U y = 5.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling