Divisibility Rule for 2

Problem 1 :

Which of these numbers are divisible by 2?

a) 216     b) 3184     c) 827    d) 4770   e) 123 456

Solution :

Any number that ends in a 0, 2, 4, 6, and 8 is can be divided by 2 to produce a whole number.

Note : So, all even numbers are divisible by 2.

a)  216 ends with the digit 6.

So, 216 is an even number and it is divisible by 2.

b) 3184 ends with the digit 4.

So, 3184 is an even number and is divisible by 2.

c) 827 ends with the digit 7.

So, 827 is not an even number, and it is not divisible by 2.

d) 4770 ends with the digit 0.

So, 4770 is an even number and is divisible by 2.

e) 123 456 ends with the digit 6.

So, 123 456 is an even number and is divisible by 2.

Problem 2 :

If a and b are odd numbers, then which of the following is even ?

a) a + b    b) a + b + 1    c) ab    d) ab + 2

Solution :

Here a and b are odd numbers, let us consider

a = 3 and b = 5

a + b => 3 + 5 ==> 8 (even)

The sum of two odd number is even.

That is, odd + odd = even

So, a + b is even.

Problem 3 :

n is a whole number when divided by 4 gives 3 as remainder What will be the remainder when 2n is divided by 4.

a) 3    b)  2      c) 1      d) 0

Solution :

Division algorithm,

Divided = divisor x quotient + remainder

Let q be the quotient.

n = 4q + 3

2n = 8q + 6

2n = 8q + 4 + 2

2n = 4(2q + 1) + 2

It exactly matches with division algorithm. Here 2q + 1 is quotient  and 2 is remainder.

Problem 4 :

A number was divided successively in order by 4, 5 and 6. The remainders were respectively 2, 3 and 4. The number is

a) 214   b)  476    c)  954   d)  1908

Solution :

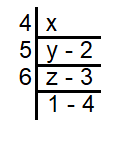
z = 6 (1) + 4

z = 10

y = 5z + 3

Applying the value of z, we get

y = 5(10) + 3 ==> y = 53

x = 4y + 2

Applying the value of y, we get

x = 4(53) + 2

x = 212 + 2

x = 214

So, the required number is 214.