DIVIDING DECIMALS BY 10 100 AND 1000

When we dividing decimals, accordingly the number of zeros that we have in 10, 100, 1000…etc. we will move the decimals. 

Dividing a decimal by 10 :

4.8 ÷ 10

Here, we have 10, it has one zero. So we have to move the decimal point to the left of one digit.

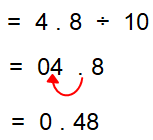
Dividing a decimal by 100 :

2.7 ÷ 100

Here, we have 100, it has two zero. So we have to move the decimal point to the left of two digit.

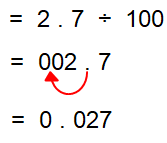
Dividing a decimal by 1000 :

0.6 ÷ 1000

Here, we have 1000, it has three zero. So we have to move the decimal point to the left of three digit.

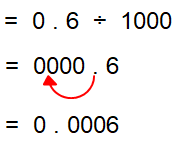
Example 1 :

Find :

a)  89 ÷ 10

b)  463 ÷ 10

c)  463 ÷ 1000

d) 463 ÷ 10000

e)  0.8 ÷ 1000

f)  0.73 ÷ 100

g)  0.07 ÷ 100

h)  0.083 ÷ 1000

i) 0.0028 ÷ 10000

j) 0.00051 ÷ 10000

Solution :

a)  89 ÷ 10

• Number of digits before the decimal = 2
• Number of 0's in 10 = 1
• Moving the decimal one digit to the left, we get 8.9

b)  463 ÷ 10

• Number of digits before the decimal = 3
• Number of 0's in 10 = 1
• Moving the decimal one digit to the left, we get 46.3

c)  463 ÷ 1000

• Number of digits before the decimal = 3
• Number of 0's in 1000 = 3
• Moving the decimal three digits to the left, we get 0.463

d) 463 ÷ 10000

• Number of digits before the decimal = 3
• Number of 0's in 10000 = 4
• Moving the decimal four digits to the left, we get 0.0463

e)  0.8 ÷ 1000

• Number of digits before the decimal = 1
• Number of 0's in 1000 = 3
• Moving the decimal three digits to the left, insufficient digits can be replaced by 0. So, we get 0.008.

f)  0.73 ÷ 100

• Number of digits before the decimal = 1
• Number of 0's in 100 = 2
• Moving the decimal two digits to the left, insufficient digits can be replaced by 0. So, we get 0.0073

g)  0.07 ÷ 100

• Number of digits before the decimal = 1
• Number of 0's in 100 = 2
• Moving the decimal two digits to the left, insufficient digits can be replaced by 0. So, we get 0.0007

h)  0.083 ÷ 1000

• Number of digits before the decimal = 1
• Number of 0's in 1000 = 3
• Moving the decimal three digits to the left, insufficient digits can be replaced by 0. So, we get 0.000083

i) 0.0028 ÷ 10000

• Number of digits before the decimal = 1
• Number of 0's in 10000 = 4
• Moving the decimal four digits to the left, insufficient digits can be replaced by 0. So, we get 0.00000028

j) 0.00051 ÷ 10000

• Number of digits before the decimal = 1
• Number of 0's in 10000 = 4
• Moving the decimal four digits to the left, insufficient digits can be replaced by 0. So, we get 0.000000051

Example 2 :

Usain Bolt won 3 gold medals in the Track and Field events in the 2012 Olympics in London. 

a) Bolt ran the 200 meters in 19.32 seconds. If he ran 100 meters at that pace, what would his 100 meter time be?

b) For 100 meters, what’s the difference between Usain’s 100 meter pace and his 200 meter pace?

c) Four Jamaican runners ran the men’s 4 × 100 meter relay with a time of 36.84. If each ran the same speed, what would one runner’s time have been?

d) If the relay runners could run as fast as Bolt did in his individual 100 meter race, would their relay time have been faster or slower? By how much?

Solution :

a) 

Time taken to complete 200 meters race = 19.32 seconds

(2 x 100) meters = 19.32

Time taken to complete 100 meters race = 19.32/2

= 9.66 seconds

b) Difference in time between 100 meter race and 200 meter race 

= 19.32 - 9.66

= 9.66 seconds

He is taking half of the time.

c) Distance covered by Jamaican = 100 meters

Time takne by all 4 = 36.84 seconds

Time takent by each of them = 36.84/4

= 9.21 seconds

d) Each individual will take 9.21 seconds. Usain Bolt is taking 9.66 seconds. So, Jamiacan is faster than Bolt.

Example 3 :

Solve the multiplication and division problems below.

a)  62 ÷ 100 = _________

b)  0.43 × 100 = _________

c)  3.4 × 1000 = _________

d)  0.08 × 0.01 = _________

e)  7.89 ÷ 0.10 = _________

f)  123.05 ÷ 100 = _________

Solution :

a)  62 ÷ 100 = 0.62

b)  0.43 × 100 = 0.0043

c)  3.4 × 1000 = 0.0034

d)  0.08 × 0.01 =

= 0.08 x 1/100

= 0.08/100

= 0.0008

e)  7.89 ÷ 0.10 =

= 7.89 ÷ (1/10)

= 7.89 x 10/1

= 78.9

f)  123.05 ÷ 100 = 1.2305

Example 4 :

Ramon bought erasers shaped like animals to give away at Family Night at his school. Each eraser costs $0.10. If he spent $25.60, how many erasers did he buy?

Write a division equation to represent this situation.

Solution :

Cost of each eraser = 0.10

Total amount spent = 25.60

Number of erasers he can obuy = 25.60/0.10

= 25.60/(1/10)

= 25.60 x (10/1)

= 256

So, he can purchase 256 erasers.