DISTRIBUTIVE PROPERTY WORD PROBLEMS

Problem 1 :

The Valley High School Auditorium is able to seat 8 elementary school groups of 65 students. Use the Distributive Property to determine how many students they can seat.

Solution:

If there are 8 groups of students.

= 8 × (60 + 5)

= 8 × 60 + 8 × 5

= 480 + 40

= 520 students

They can seat 520 students.

Problem 2 :

Five friends each buy a shirt that costs x dollars and a pair of shoes that cost $24.00. Write an expression to show how much total money they spent. Then rewrite the expression using the Distributive Property.

Solution:

Total cost of shirt and shoes = (24 + x) 

Total money spent = 5 × (24 + x) 

Total money spent = (5 × 24) + (5 × x)

= 5x + 120

Problem 3 :

A rental company buys 7 more compact cars for $8,500 each and 7 more midsize cars for $12,500 each. How much total money will they spend?

Solution:

Total money spent = 7 × (8500 + 12500)

= 7 × 21000

=147000

They spent 147000 dollars.

Problem 4 :

A baking company charges $1.75 per slice for baking and $0.35 per slice for decorating. How much would a decorated cake cost containing 150 slices?

Solution:

Total cost = 150 × (1.75 + 0.35)

= 150 × 2.1

= 315

A decorated cake would cost 315 dollar containing 150 slices.

Use the table that shows the umber of seats available on various types of aircrafts.

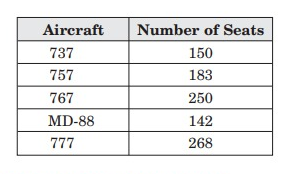
Problem 5 :

How many total seats will the airline gain by purchasing three more of both the 737 aircrafts and MD-88 aircrafts?

Solution:

Total number of seats in three 737 aircrafts = 3 × 150 = 450

Total number of seats in three MD-88 aircrafts = 3 × 142 = 426

= 450 + 426​​

Total number of seats gained is 876 seats.

Problem 6 :

How many more people can sit on four 777 aircrafts than on four 767 aircrafts?

Solution:

Number of seats in four 777 aircrafts = 268 × 4 = 1072

Number of seats in four 767 aircrafts = 250 × 4 = 1000

= 1072 − 1000

72 many more people can sit on four 777 aircrafts than on four 767 aircrafts.

Problem 7 :

The price for each textbook is p. The number of notebooks bought by Lily, Jim and Jessica is a, b and c. Write an expression to represent the total cost of all the notebooks bought by 3 people.

Solution :

Price of each text book = p

Number of books bought by Lily = a

Number of books bought by Jim = b

Number of books bought by Jessica = c

Total number of books = a + b + c

Total cost = p(a + b + c)

Problem 8 :

The price each meter of wire is u, and there are 3 parts of wires whose length are x, y and z. Write the expression which represents the cost of buying the 3 parts of wire.

Solution :

Price of each meter of wire = u

Length of three parts of wire are x, y and x.

Cost of buying 3 parts = u(x + y + z)

Problem 9 :

For two days, your boss decides to double the commission on what you sell. If on day 1, you make f dollars in commission and and day 2, you make g dollars in commission, write an expression for the total commission you earn.

Solution :

Sales made on day 1 = f

Sales made on day 2 = g

Total sales = f + g

Total commission = 2(f + g)