DIFFERENT TYPES OF RELATIONS IN MATH

Let

S = {a, b, c.......}

be any set then the relation R is a subset of the product set S x S.

Note :

A relation which is reflexive, symmetric and transitive is called an equivalence relation or simply an equivalence is equal to is an equivalence relation.

Problem 1 :

Let

𝑆 = {(𝑎, 𝑎), (𝑎, 𝑐), (𝑏, 𝑏), (𝑏,𝑒), (𝑐, 𝑎), (𝑐, 𝑐), (𝑑, 𝑑), (𝑒, 𝑏), (𝑒,𝑒)}

be a relation defined on the set 𝐴 = {𝑎, 𝑏, 𝑐, 𝑑,𝑒}

Check if the relation 𝑆 is an equivalence relation

Solution :

Reflexive :

Symmetric :

𝑆 = {(𝑎, 𝑎), (𝑎, 𝑐), (𝑏, 𝑏), (𝑏,𝑒), (𝑐, 𝑎), (𝑐, 𝑐), (𝑑, 𝑑), (𝑒, 𝑏), (𝑒,𝑒)}

• (𝑎, 𝑐) exists, (c, a) also exists.
• (b, e) exists, (e, b) also exists.

S is a symmetric relation.

Transitive :

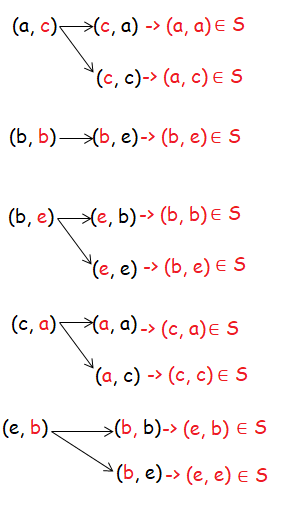
S is transitive relation. So, the given relation S is equivalence relation.

Problem 2 :

Check the relation is whether, reflexive, symmetric or transitive.

Let A = {1, 2, 3}

R₁ = { (1, 1) (2, 2) (3, 3) (1, 2) }

Solution :

Reflexive :

Set A contains 3 elements 1, 2 and 3.

(1, 1)

(2, 2) (3, 3) ∈ A

The relation is reflexive.

Symmetric :

• (1, 1) ∈ A, then (1, 1) ∈ A
• (2, 2) ∈ A, then (2, 2) ∈ A
• (3, 3) ∈ A, then (3, 3) ∈ A

(1, 2) ∈ A, then (2, 1) does not exists. So, the relation is  not symmetric.

Transitive :

• (1, 1) ∈ A, (1, 2) ∈ A, then (1, 2) should also exist on A.
• (2, 2) ∈ A, (2, 2) ∈ A, then (2, 2) should also exist on A.
• (3, 3) ∈ A, (3, 3) ∈ A, then (3, 3) should also exist on A.
• (1, 2) ∈ A, (2, 2) ∈ A, then (1, 2) should also exist on A.

Then the relation is reflexive and transitive but not symmetric.

Problem 3 :

Check the relation is whether, reflexive, symmetric or transitive.

Let A = {1, 2, 3}

R₂ = { (1, 1) (2, 2) (1, 2) (2, 1) }

Solution :

Reflexive :

Set A contains 3 elements 1, 2 and 3.

(1, 1), (2, 2) ∈ A but (3, 3) does not exists in A. So, it is not reflexive.

Symmetric :

• (1, 1) ∈ A, then (1, 1) ∈ A
• (2, 2) ∈ A, then (2, 2) ∈ A
• (1, 2) ∈ A, then (2, 1) ∉ A

Then the relation A is not symmetric.

Transitive :

• (1, 1) ∈ A, (1, 2) ∈ A, then (1, 2) also exists on A.
• (2, 2) ∈ A, (2, 1) ∈ A, then (2, 1) also exists on A.
• (1, 2) ∈ A, (2, 2) and (2, 1) ∈ A, then (1, 2) (1, 1) should also in A.
• (2, 1) ∈ A, (1, 1) and (1, 2) ∈ A, then (2, 1) (2, 2) should also in A.

Problem 4 :

Check the relation is whether, reflexive, symmetric or transitive.

Let A = {1, 2, 3}

R₃ = { (1, 1) (2, 2) (3, 3) (1, 2) (2, 1)(2, 3) (3, 2) }

Solution :

Reflexive :

Set A contains 3 elements 1, 2 and 3.

(1, 1), (2, 2), (3, 3) does not exists in A. So, it is reflexive.

Symmetric :

• (1, 1) ∈ A, then (1, 1) ∈ A
• (2, 2) ∈ A, then (2, 2) ∈ A
• (3, 3) ∈ A, then (3, 3) ∈ A
• (1, 2) ∈ A, then (2, 1) should also in A. It is.
• (2, 1) ∈ A, then (1, 2) should also in A. It is.
• (2, 3) ∈ A, then (3, 2) should also in A. It is.
  
• (3, 2) ∈ A, then (2, 3) should also in A. It is.
  

Then the relation A is symmetric.

Transitive :

• (1, 2) ∈ A, (2, 2) and (2, 1) ∈ A, then (1, 2) and (1, 1) should also on A and it is.
• (2, 1) ∈ A, (1, 1) and (1, 2) ∈ A, then (2, 1) and (2, 2) should also in A and it is.
• (2, 3) ∈ A, (3, 2) and (3, 3) ∈ A, then (2, 2) and (2, 3) should also in A and it is.
• (3, 2) ∈ A (2, 2) and (2, 1) ∈ A, then (3, 2) and (3, 1) should also in A. But (3, 1) does not exist on A. Then it is not transitive.

The function is symmetric and reflexive but not transitive.

Problem 5 :

Let A = {1, 2, 3} and R = {(1, 2) (2, 2)(3, 1)(3, 2)}

From the given relation, find domain and range of function and inverse function.

Solution :

Set of first values (inputs) from the ordered pairs is domain.

Set of second values (outputs) from the ordered pairs is range.

R = {(1, 2) (2, 2)(3, 1)(3, 2)}

Domain of R = {1, 2, 3}

Range of R = {1, 2}

Domain of R = Range of R^-1

Range of R = Domain of R^-1

Domain of R^-1 = {1, 2}

Range of  R^-1 = {1, 2, 3}